Властивість бути канторовою множиною є топологічним інваріантом. Це означає, що якщо A гомеоморфна B, причому A – компактна, досконала і цілком незв’язна, то B також компактна, досконала і цілком незв’язна.
Доведення. Нехай f – гомеоморфізм із A на B. Так як множина A – компактна, а відображення f неперервне, то по теоремі 1.2 множина B = f(А) також компактна.
Згідно з теоремою 1.3, зв’язність є топологічним інваріантом. Якщо C – компонента f (B), то f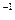 
(C) є зв’язна множина в A. Так як A – цілком незв’язна, то її складовими є окремі точки. Таким чином, C повинна бути окремою точкою. Звідси слідує, що B також незв’язна.
Так як A досконала, то A замкнена і не має ізольованих точок. Оскільки B компактна, то вона є замкненою. Припустимо, що y = f (x) – ізольована точка B. Тобто існує множина U, відносно відкрита в B, яка не містить ніяких інших точок з B, крім у. Але тоді f 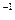(U) буде відносно відкритою множиною в A і не міститиме ніяких інших точок з A, крім x, щo призводить до протиріччя умові (множина A – досконала). Отже множина B не має ізольованих точок, а тому вона досконала. Доведено.
Зауваження 1. Очевидно, що всі наведені вище приклади множин є об'єктами, гомеоморфними класичному пилу Кантора.
Зауваження 2. Топологічні відображення (гомеоморфізми) не зберігають метричних властивостей множин. Для наочності цього факту уявимо фрактал, що намальований на гумовій стрічці, котра потім нерівномірно розтягується в різних напрямках. Отримана фігура гомеоморфна оригіналові, але такі властивості, як самоподібність і фрактальна розмірність не зберігаються.
Дата добавления: 2015-08-21; просмотров: 106 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Н е п е р е р в н о с т і. | | | Застосування множин, гомеоморфних множині Кантора |