В і н о ч о к

Означення 7.Візьмемо послідовність і множину коренів шостого степеня з одиниці , . Кожному числу , записаному в шістковій системі числення, яке належить відрізку [0,1] і має нескінченну кількість цифр після коми, поставимо у відповідність точку комплексної площини .

Множина точок комплексної площини, утвореної за таким правилом називається віночком (діаметра 2) (рис. 2.24). (Цей спосіб побудови та задання фрактальних об’єктів був запропонований професором Працьовитим М.В.).

Рис 2.24.

Означення 8. Віночком називається орбіта групи перетворень , де 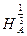- гомотетія з центром в точці і коефіцієнтом , - поворот навколо деякої довільної, наперед заданої точки на кут .

Теорема 2.1. Віночок разом із частиною площини, яку він обмежує, утворює острівець Коха.

Доведення. Згідно з означенням сніжинки Коха і означення віночка, кожна точка сніжинки Коха є точкою віночка. Але, оскільки діаметри сніжинки Коха і віночка співпадають, то віночок разом із частиною площини, яку він обмежує, утворює острівець сніжинки Коха. Доведено.

Означення 9. Розділимо острівець сніжинки Коха на сім острівців сніжинок Коха (згідно властивості оcтрівця сніжинки Коха, це можна зробити) так, що центральний острівець подібний до початкового з коефіцієнтом подібності , а шість інших – з коєфіцієнтом подібності (згідно доведення властивості острівця сніжинки Коха, це можна зробити), і викинемо центральний острівець сніжинки Коха, залишивши його межу. Отриману фігуру назвемо заповненим віночком.

Дата добавления: 2015-08-21