
Процес побудови. Вихідна фігура – правильна піраміда. Почнемо наш процес побудови з однієї з граней піраміди. Нехай К0 – початковий рівносторонній трикутник з основою а (рис. 2.27(а)). Поділимо основу трикутника на три рівних частини і побудуємо рівносторонній трикутник з основою (рис.2.27(б)). Виймемо його з К0 і добудуємо два нових трикутника (рис. 2.27(в)). Назвемо отриману множину К1. Повторимо цю процедуру багатократно. Позначимо через Кn – фігуру отриману на n-му кроці. Послідовність 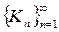 збігається до деякої граничної фігури К. Назвемо її модель конічного виду.
збігається до деякої граничної фігури К. Назвемо її модель конічного виду.


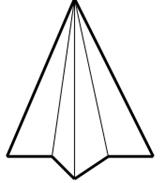
Рис. 2.27(а). Рис. 2.27(б). Рис. 2.27(в).
Розмірність. Оскільки модель конічного виду не є самоподібним фракталом, то розмірність самоподібності способом, аналогічним способу обрахунку розмірності циліндричної моделі обрахувати неможливо.
Площа поверхні та об’єм, обмежений даною фігурою. Знайдемо площу поверхні цієї фігури.
Sпов.= Sбічне + Sосн.  S осн.
S осн.  ,
,
де а – сторона рівностороннього трикутника, що лежить в основі піраміди. Нехай S0 – площа бічної поверхні правильної піраміди.  площа кожної грані.
площа кожної грані.
На першому кроці утворюється фігура, що матиме 12 граней, кожна з яких має площу  , тому:
, тому:
S1=  .
.
На другому кроці:
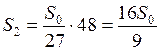 .
.
На n -му кроці:
 .
.
Та процес побудови на цьому кроці не завершується, ми продовжуємо його нескінченно довго:
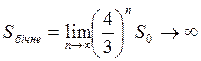

Отже, площа поверхні об’єкта необмежено зростає.
Тепер знайдемо об’єм, обмежений цією фігурою.
Він дорівнює 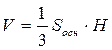 . Оскільки частина площини, яку обмежує сніжинка Коха, має площу
. Оскільки частина площини, яку обмежує сніжинка Коха, має площу  , де
, де 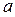 – довжина початкового, рівностороннього, трикутника, то:
– довжина початкового, рівностороннього, трикутника, то:

Отже, наша фігура володіє такою властивістю: якщо процес побудови проводити нескінченно довго, площа поверхні такого об’єкта нескінченно зростає, хоча об’єм, обмежений такою поверхнею – скінченний.
2.6.3. Б р у н ь к о в а м о д е л ь. Брунькова модель– це модель, побудована з тетраедрів, в чотирьох не паралельних перерізах якої лежать сніжинки Коха.
Спосіб побудови. Вихідною фігурою є тетраедр з ребром а. На першому етапі на кожному ребрі, а саме на його середній третині, надбудовуємо 2 тетраедри з ребром  (рис. 2.28).
(рис. 2.28).

Рис. 2.28.
При цьому грань А5А7А8 тетраедра А6А5А7А8 лежить в одній площині з гранню А4А2А3 вихідного тетраедра, а грань А5А9А8 тетраедра А10А5А9А8 лежить в одній площині з гранню А1А2А3 (рис. 2.29).

Рис. 2.29.
Оскільки граней шість, то всього надбудовується дванадцять тетраедрів з ребром а /3. Таким чином ми одержимо у чотирьох не паралельних перерізах сніжинку Коха на першому кроці побудови. На другому кроці на кожне з сімдесяти двох ребер надбудовується по два тетраедра з ребром а /9. Для прикладу зробимо надбудову на ребро А5А9 ( рис. 2.30).

Рис. 2.30.
Бачимо, що грані А11А14А15 тетраедра А11А14А15А16 лежить в одній площині з гранню А5А9А8 тетраедра А5А9А8 А10; грань А11А13А15 тетраедра А11А12А13А15 лежить в одній площині з гранню А5А9А8 тетраедра А5А9А8 А10, а також з гранню А1А2А3 вихідного тетраедра. Зробивши всі сімдесят дві надбудови, ми отримаємо в чотирьох перерізах сніжинку Коха другого кроку побудови. Так цей процес проводиться до нескінченності (по принципу сніжинки Коха на площині). В результаті одержано фігуру, побудовану з тетраедрів, в чотирьох непаралельних перерізах якої будуть лежати сніжинки Коха.
Кількість надбудованих тетраедрів на n-му кроці. Кількість надбудованих тетраедрів на n-му кроці побудови порахуємо виходячи з таких міркувань: після побудови двох тетраедрів одержимо дванадцять ребер.
На нульовому кроці ми маємо один тетраедр. На першому кроці побудови на кожне з шести ребер тетраедра ми надбудовуємо по два тетраедри, тому всього їх буде дванадцять. Шість пар надбудованих тетраедрів будуть давати сімдесят два ребра, кожна пара тетраедрів дає дванадцять ребер. Оскільки на другому кроці побудови на кожне ребро надбудовується по два тетраедра, то загальна їх кількість буде  . Ці сто сорок чотири тетраедра будуть давати
. Ці сто сорок чотири тетраедра будуть давати  ребра. Таким чином на третьому кроці побудови, загальна кількість надбудованих тетраедрів буде рівна
ребра. Таким чином на третьому кроці побудови, загальна кількість надбудованих тетраедрів буде рівна  . Легко бачити, що на (n-1)-му кроці побудови кількість ребер буде
. Легко бачити, що на (n-1)-му кроці побудови кількість ребер буде  . А кількість надбудованих тетраедрів на n-му кроці буде рівна
. А кількість надбудованих тетраедрів на n-му кроці буде рівна 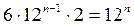 .
.
Кут між двома надбудованими тетраедрами, що лежать на одному ребрі. Кут між двома надбудованими тетраедрами, що знаходяться на одному ребрі, це двогранний кут  ANS правильної піраміди SABC (рис. 2.31(а,б)).
ANS правильної піраміди SABC (рис. 2.31(а,б)).

Рис. 2.31(а).

Рис. 2.31(б).
Нехай АВ = а, тоді AN 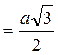 , АР = а /2. З
, АР = а /2. З  ANSвидно, що
ANSвидно, що 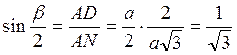 (рис. 2.32),
(рис. 2.32),  .
.
Отже, кут між двома тетраедрами, що розміщені на одному ребрі, дорівнює  .
.

Рис. 2.32.
Площа поверхні та об’єм, обмежений даною фігурою. Нехай S0 – площа поверхні вихідного тетраедра. Оскільки на першому кроці побудови надбудовують дванадцять тетраедрів, кожен з яких має площу у дев’ять разів меншу за площу вихідної фігури, то загальна площа тетраедрів першого кроку побудови буде рівна
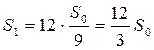 .
.
На другому кроці фігура має сто сорок чотири надбудованих тетраедри, площа кожного з них –  , тому
, тому
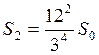 .
.
На n –му кроці добудовується  тетраедрів площа яких рівна
тетраедрів площа яких рівна  ,тому
,тому  . Тоді площа поверхні буде рівна:
. Тоді площа поверхні буде рівна:
S=S0+S1+S2+... +Sn+... = S0+ 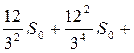 ...
...  .
.
Ми бачимо, що це ряд, члени якого утворюючи геометричну прогресію зі знаменником прогресії  . Оскільки
. Оскільки 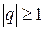 , то границя ряду розбіжна. Отже, площа поверхні такого об’єкту нескінченно зростає.
, то границя ряду розбіжна. Отже, площа поверхні такого об’єкту нескінченно зростає.
Тепер знайдемо об’єм, обмежений цією фігурою.
Нехай V 0 - об’єм вихідного тетраедра. Об’єм тетраедрів, надбудованих на першому кроці буде рівний  , оскільки їх загальна кількість дванадцять, а об’єм кожного з них менший за об’єм вихідної фігури в вісімдесят один раз.
, оскільки їх загальна кількість дванадцять, а об’єм кожного з них менший за об’єм вихідної фігури в вісімдесят один раз.
На 2 -му кроці побудови надбудовується 144 тетраедра, кожен з яких має об’єм  , тому
, тому 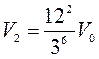 .
.
На n -му кроці побудови надбудовується 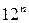 тетраедрів, кожен з яких має об’єм
тетраедрів, кожен з яких має об’єм  , тому
, тому  .
.
Тоді об’єм, що обмежує ця поверхня, буде рівний  Отже, наша фігура володіє такою властивістю: якщо процес побудови проводити нескінченно довго, площа поверхні такого тетраедра необмежено зростає, хоча об’єм обмежений цією поверхнею – скінченний.
Отже, наша фігура володіє такою властивістю: якщо процес побудови проводити нескінченно довго, площа поверхні такого тетраедра необмежено зростає, хоча об’єм обмежений цією поверхнею – скінченний.
2.6.4. К а р к а с б р у н ь к о в о ї м о д е л і. Тепер розглянемо каркас брунькової моделі – фігуру побудовану не з тетраедрів, а лише з їх ребер. Знайдемо розмірність та довжину цієї кривої.
Розмірність. Кожне з шести ребер вихідної фігури ділимо на три рівних частини. На кожному із середніх відрізків добудовуємо ребра двох тетраедрів (рис. 2.33).
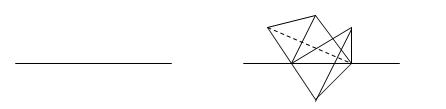
Рис. 2.33.
Таким чином, поділивши ребро вихідної фігури на три (n=3), ми отримаємо тринадцять відрізків нового етапу поділу (N=13). Тому  2,334.
2,334.
Отже, дана крива складається з шести самоподібних фракталів розмірності  .
.
Довжина кривої. Знайдемо довжину одного із шести фракталів. Нехай вихідний відрізок К0 має довжину l, тоді довжина кривої К1 рівна 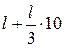 . Довжина кривої К2 рівна
. Довжина кривої К2 рівна 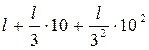 . Продовжуючи таким чином маємо, що крива Кn після n -го кроку маємо довжину
. Продовжуючи таким чином маємо, що крива Кn після n -го кроку маємо довжину  . Ми одержали ряд, члени якого утворюють геометричну прогресію зі знаменником
. Ми одержали ряд, члени якого утворюють геометричну прогресію зі знаменником  . Оскільки
. Оскільки  , то границя ряду розбіжна. Отже, довжина граничної кривої К рівна нескінченості.
, то границя ряду розбіжна. Отже, довжина граничної кривої К рівна нескінченості.
Дата добавления: 2015-08-21; просмотров: 112 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дослідження аналогів зірки Коха у тривимірному просторі | | | Кубічне узагальнення сніжинки Коха |