Двовимірне узагальнення килима Серпінського

Що вийде, якщо поділити квадрат на дев’ять рівних квадратів і вилучати не середній квадрат, а будь-який інший квадрат або квадрати?

В результаті можна отримати, очевидно, самоподібних об’єктів включаючи килим Серпінського, цвинтар Серпінського і множину Кантора. Їх площа буде такою ж як і у килима Серпінського. Спосіб підрахунку площ аналогічний до підрахунку площі килима Серпінського. Будемо вважати однаковими ті з них, які отримуються один з одного шляхом симетрії відносно всіх ліній симетрії початкового квадрата або (та) поворотом на кут кратний відносно центру квадрата.

Підрахуємо скільки таких різних об’єктів існує. Для цього скористаємося теоремою Пойа [15]. Отже, утворимо твірну функцію запасу для самосуміщень квадрату. Маємо:

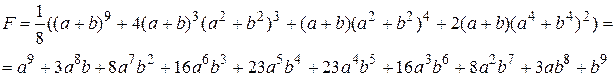
Дана функція дозволяє визначити скільки існує об’єктів даної розмірності. Наприклад, треба визначити скільки існує об’єктів розмірності 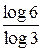. Для цього треба знайти коефіцієнт біля 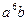. Отже, об’єктів розмірності 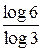існує рівно 16.

Тому, знайшовши суму всіх коефіцієнтів визначимо, що всього таких об’єктів 102, але серед них є квадрат і порожня множина, тобто залишається рівно 100 об’єктів [5].

Варіанти перших етапів побудови різних об’єктів зображено на рис. 3.3.

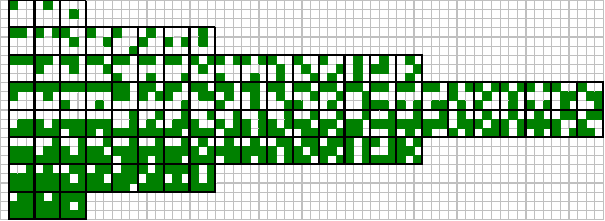
Рис. 3.3.

Отримані об’єкти можна погрупувати за розмірностями. На рис 3.3. об’єкти з однаковою розмірністю розташовані в одному рядку.

В додатку А наведені деякі фрактальні множини, які отримуються шляхом вилучення з квадрата менших квадратів.

Дата добавления: 2015-08-21