Зв’язок трикутника Паскаля з трикутником Серпінського

Ряди трикутника Паскаля умовно пронумеровані згори, починаючи з нульового, й числа в нижньому ряді відносно чисел у попередньому ряді завжди розміщені ступінчато й навскіс. Побудувати цей трикутник просто. Кожне число в кожному ряді одержуємо, додавши два числа, розміщені вгорі (зліва і справа). Якщо зліва або справа немає числа, підставляємо нуль на його місце. Наприклад, перше число в першому ряді , тоді, як числа і в третьому ряді утворюють число 4 в четвертому ряді: [1]. На рис. 1.1 зображено перші 14 рядків трикутника Паскаля.

Рис. 1.1. Перші 14 рядків трикутника Паскаля.

Трикутник Паскаля за

Якщо при побудові трикутника Паскаля записувати замість чисел їхню остачу від ділення на два, то на місці парних чисел буде , непарних – (рис. 1.2).

Рис. 1.2. Трикутник Паскаля за .

Спостерігаємо, що трикутник Паскаля за утворює трикутний килим Серпінського.

Трикутник Паскаля за

Аналогічно, якщо при побудові трикутника Паскаля записувати замість чисел їхню остачу від ділення на три, то на місці чисел, кратних , буде , (рис. 1.3).

Рис. 1.3. Трикутник Паскаля за .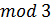

Спостерігаємо, що трикутник Паскаля за 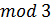утворює третинний трикутний килим Серпінського.

1.1.1. Трикутник Паскаля за

Аналогічно, якщо при побудові трикутника Паскаля записувати замість чисел їхню остачу від ділення на , то на місці чисел, кратних , буде .

З вищевикладеного робимо висновок, що отримаємо -тинний трикутний килим Серпінського.

Отже, трикутний килим Серпінського можна будувати не лише «стандартно», його можна будувати також ділячи на 3, на 5, на 7 та і взагалі на будь-яке число, але в нашому випадку розглянутий трикутний килим Серпінського при поділі на будь-яке просте число .

Трикутник Паскаля за утворює трикутний килим Серпінського. Аналогічно, трикутник Паскаля за 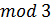утворює третинний килим Серпінського, трикутник Паскаля за 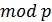утворює -тинний трикутний килим Серпінського.

---

Дата добавления: 2015-08-21