Побудова кривої Пеано

Сніжинку Коха та інші неперервні криві на площині, отримані з допомогою L -систем [8:23], об’єднує те, що їх розмірність задовольняє нерівності: . Виникає питання, чи існує крива розмірності Це питання цікаве не тільки тим, що відповідь на нього позитивна, але і тим, що воно було розв’язане Джузеппе Пеано ще в 1890 році. Пеано побудував неперервну функцію, область визначення якої – відрізок, а область значень – квадрат на площині. Відповідна лінія називається кривою Пеано або кривою, яка заповнює площину. Крива Пеано не є фракталом у визначенні Мандельброта, але все-таки цікава як приклад функції, яка відображає множину заданої розмірності на множину більшої розмірності. Ці та інші подібні відкриття того часу, особливо роботи Вейєрштраса і Кантора, справили великий вплив на подальший розвиток математичного аналізу. Поняття кривої Пеано, безумовно, не є інтуїтивним, а початково з’явилося із чисто аналітичних міркувань.

Наведемо означення кривої Пеано, яке пропонується в книзі Р. Кроновера [8;46].

Введемо позначення, зручні при вивченні властивостей кривої Пеано. Нехай І – одиничний відрізок [0,1], S – одиничний квадрат І×І, тобто:

S = {(x,y) | x,y Î І}.

При побудові використовується представлення точок відрізка І в системі числення за основою 9. Перший крок полягає в тому, щоб розбити S на дев’ять рівних частин. Неперервна крива, що проходить через всі квадрати, будується так, як показано на рисунку 4.1 лінією з стрілками, пунктирна лінія показує в якому порядку обходяться квадрати. Квадрати занумеровані числами 0, 1, 2, 3, 4, 5, 6, 7 і 8, відповідно до порядку, в якому лінія їх перетинає. Отримана лінія є першою ітерацією побудови. Далі кожен з цих дев’яти квадратів розбивається на дев’ять підквадратів, що нумеруються аналогічно. Отримуємо лінію, що проходить через дев’ять підквадратів таким чином, що її початкова і кінцева точка накладаються на криву попереднього рівня. Це дозволяє нам занумерувати підквадрати числами 0, 1, 2, 3, 4, 5, 6, 7 та 8 всередині кожного квадрату. Повторимо цю процедуру нескінченно. Фактично, крива Пеано визначається відображенням, яке ставить точці xÎІ, записаній в дев’ятірковій системі числення 0,x₁x₂x₃...., точку P(x) є S за правилом:

Р(х) – в квадраті під номером x₁ після першої ітерації,

Р(х) – в квадраті під номером x₁x₂ після другої ітерації,

Р(х) – в квадраті під номером x₁x₂x₃ після третьої ітерації

...

Теорема 4.1. Відображення Пеано є неперервна функція, яка переводить інтервал I в квадрат S. Більш того, послідовність відображень 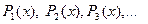збігається: .

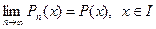Рис. 4.1. Друга ітерація побудови Пеано, .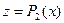

Доведення. Ми доведемо сильніше твердження, ніж просто існування границі 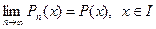. Встановимо, що збіжність на відрізку I –рівномірна, із чого можна буде зробити висновок про неперервність граничної функції. Для встановлення рівномірної збіжності застосуємо критерій Коші в такому формулюванні.

Для кожного існує такий номер , що при виконується нерівність: 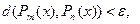для всіх , де 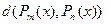– евклідова відстань між точками .

Нехай . Розглянемо сітку , яка натягнута на точки вигляду: . Нехай , і точки розбивають відрізок на інтервалів рівної довжини. Зауважимо, що переміщається по діагоналі одного із квадратів сітки при зміні х від до . З іншого боку, обов’язково знаходяться в тому ж квадраті, якщо . Отже, для : .

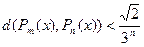Дане міркування не залежить від того, якому саме інтервалу належить точка х, а значить, нерівність вірно для всіх . Таким чином, вибравши К із умови , ми задовольнимо нерівність 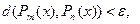для всіх при . Доведено.

Інший спосіб побудови кривої запропоновано Д. Гільбертом. Завдання полягає в тому, щоб поставити у відповідність кожній точці відрізка Т деяку точку квадрата Q і притому так, щоб кожна точка квадрата відповідала деякій точці відрізка. Відображення відрізка, яке нас цікавить повинно бути, крім того, і неперервним, тобто задовольняти тій умові, щоб достатнім зближенням точок відрізка можна було домогтися того, щоб відповідні їм точки квадрата були як завгодно близькі. От як будується це відображення. Розіб’ємо відрізок Т на чотири рівні частини і позначимо часткові відрізки в порядку їхній проходження зліва праворуч буквами , , , . Точно так само розіб’ємо квадрат Q на чотири рівних квадрата і позначимо ці квадрати через , , , 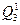. Відрізки , , і відповідні їм квадрати будемо називати відрізками і квадратами першого рангу. 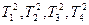Розіб’ємо далі кожний із відрізків , , знову на чотири рівні частини і позначимо частини і відрізки, що утворюються розбивкою відрізка , послідовно через ; відрізки, на які розбивається , позначимо послідовно через , ; розбивку відрізка , позначимо через розбивку відрізка – через ; 16 відрізків, що утворюються при цій другій розбивці, будемо називати відрізками другого рангу. Розіб’ємо, далі, кожний із чотирьох квадратів на чотири рівних квадрати. Ми одержимо 16 квадратів другого рангу. Квадрати, на які розіб’ється квадрат , позначимо через , розбивку квадрата позначимо через , розбивку 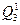- через і розбивку – через . При цьому ми повинні вибирати позначення так, щоб квадрати, у яких нижні покажчики відрізняються на 1, неодмінно мали принаймні одну спільну точку. Але томущо чотири квадрати, які утворюються розбивкою одного квадрата першого рангу, завжди мають спільну точку – центр цього квадрата, то при виборі позначень треба стежити тільки за тим, щоб мали спільні точки кожні два квадрати, тобто останній і перший квадрати другого рангу, що є розбивкою сусідніх квадратів першого рангу (рис. 4.2).

Рис. 4.2.

Пунктирна лінія вказує, в якому порядку проходяться квадрати, коли відрізки проходяться послідовно зліва праворуч.

Розіб’ємо тепер кожний із відрізків другого рангу на чотири рівні відрізки. Ми одержимо 64 відрізки третього рангу, які позначимо послідовно (зліва праворуч) через ,..., ; аналогічно розіб’ємо кожний із 16 квадратів другого рангу на чотири рівні квадрати. Одержимо 64 квадрати третього рангу. Позначимо їх відповідно так само, як і відрізки (рис. 4.3).

Зауважимо, що при позначенні кожні два сусідні квадрати третього рангу (нижні показники яких відрізняються на 1) повинні мати спільну точку. Але оскільки кожні чотири квадрати третього рангу завжди мають спільну точку (центр цього квадрата), то потрібно стежити лише за тим, щоб кожний квадрат третього рангу, що є останнім у розбивці деякого квадрата другого рангу, мав спільну точку з першим квадратом третього рангу, що входить у розбивку сусіднього квадрата другого рангу.

Рис. 4.3.

Пунктирна лінія вказує порядок проходження квадратів, що відповідає проходженню відрізків зліва праворуч.

Описаний процес розбивки відрізків і квадрати ми можемо продовжувати безмежно; при цьому зі зростанням номера рангу розбивки як довжини відрізків, так і сторони квадратів будуть наближатися до нуля, тому

що для розбивки рангу п довжини відрізків будуть рівні , а довжини сторін квадрата будуть . Поставимо тепер у відповідність кожному відрізку рангу п квадрат Q того ж рангу, що має той же номер k, що і даний відрізок. Ми одержимо тоді для кожного рангу п взаємно однозначну відповідність між відрізками і квадратами розбивки цього рангу. Ця відповідність між відрізками і квадратами і дозволить побудувати цікавляче нас неперервне відображення відрізка Т на квадрат Q. Нехай – яка-небудь точка відрізку. Ця точка належить принаймні одному (і не більш ніж двом) відрізку першого рангу, принаймні одному відрізку другого рангу, принаймні одному відрізку третього рангу, і т.д. Візьмемо квадрати, що відповідають відрізкам, що містять точку . Ми одержимо нескінчену послідовність квадратів. Тому що кожний квадрат рангу утримується в деякому квадраті попереднього рангу і тому що зі зростанням номера рангу довжина сторони прямує до нуля, то всі ці квадрати мають тільки одну спільну точку , що ми і поставимо у відповідність точці . Отже, ми показали, що кожній точці відрізка відповідає одна цілком визначена точка квадрата.

Нам потрібно тепер показати, що при такій відповідності кожна точка квадрата відповідає принаймні одній точці відрізка. Нехай - довільна точка квадрата Q. Вона належить принаймні одному квадрату першого рангу, принаймні одному квадрату другого рангу, що утримується в квадраті третього рангу і т.д.

Проте, та сама точка квадрата може відповідати декільком різноманітним точкам відрізка, тобто наша відповідність не є взаємно однозначним. Такими точками квадрата, кожна з який відповідає декільком точкам відрізка, є вершини квадратів розбивок усіх рангів: кожна така вершина відповідає чотирьом різноманітним точкам відрізка, за винятком центру квадрата Q, що відповідає лише трьом різноманітним точкам відрізка. Такою ж властивістю – відповідати декільком точкам відрізка - володіє кожна точка сторони квадрата розбивки будь-якого рангу, і тільки ті точки, що є внутрішніми для квадратів усіх рангів, володіють тим властивістю, що кожна з них відповідає лише одній точці відрізка.

Роздивимося відрізки, що відповідають цим квадратам. Кожний із цих відрізків утримується в попередньому, причому довжина відрізка з ростом номера рангу розбивки наближається до нуля. Отже, усі ці відрізки мають лише одну спільну точку . Цій точці відрізка Т і відповідає точка квадрата Q.

Нам залишається довести безперервність побудованого відображення. Але якщо - яка-небудь точка відрізку, то при любому n усяка точка t цього відрізка, достатньо близька до точки , буде лежати з нею на тому самому відрізку рангу n або на сусідньому відрізку того ж рангу. Але тоді і відповідним точкам і t відрізка Т точки і m квадрата Q будуть належати одному або сусіднім квадратам того ж рангу. Тому, якщо брати точки t достатньо близькими до точки , то відповідні їм точки m можна зробити як завгодно близькими до точки , що і доводить неперервність відображення [17].

Отримане нами відображення відрізку на квадрат дозволить побудувати “криву” Пеано. Справді, якщо за відрізок Т узяти відрізок числової осі 0<t<l, а за квадрат Q - одиничний квадрат площини XOY, координати точок якого визначаються нерівностями 0<х<1, 0<у<1, то побудоване тільки що відображення відрізка на квадрат породжує дві неперервної функції x= , y= 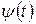які утворюються, якщо кожному значенню t поставити у відповідність координати тієї точки m, що відповідає цьому значенню t при даному неперервному відображенні.

Неперервність функцій випливає з того, що якщо узяти точки і t відрізка Т достатньо близькими, то і відповідні їм точки і m будуть як завгодно близькі, із чого у свою чергу випливає, що як їхньої абсциси, так і їхні ординати будуть як завгодно мало відрізнятися один від одного.

Так утворюється приклад “кривої”, заданої параметричними рівняннями, що “проходить” через усі точки квадрата.

Як ми вже говорили, розглянуте нами неперервне відображення відрізка на квадрат не є взаємно однозначним; існує нескінченна множина точок квадрата, кожна з який відповідає декільком (двом, трьом або чотирьом) точкам відрізку. Можна було б показати, що це не залежить від способу, яким здійснюється неперервне відображення відрізка на квадрат: при всякому такому відображенні завжди знайдуться точки квадрата, кожна з який відповідає декільком точкам відрізка.

Крім цього крива Пеано являє собою самоподібний об’єкт з коефіцієнтом подібності . Визначимо розмірність самоподібності. Рівняння самоподібності має вигляд , де к – кількість об’єктів на яку розбивається фігура на першому етапі побудови, m – коефіцієнт подібності. Крива Пеано заповнює квадрат, який на першому етапі розбивається на чотири квадратики, тобто k = 4, коефіцієнт подібності рівний , бо кожен з квадратиків, на які розбивається великий квадрат, в двічі менший за нього, отже, 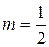звідси отримуємо рівняння:

,

звідки слідує, що x = 2. Отже крива Пеано має розмірність 2.

Дата добавления: 2015-08-21