Ч о т и р и в и м і р н и й п и л К а н т о р а

Описовий спосіб задання. Цю фігуру ми будуємо так, беремо гіперкуб і ділимо його на 81 конгруентних йому гіперкуби, а потім, на першому кроці побудови, ми викидаємо 1 центральний гіперкуб і 64 прилеглих до нього гіперкуба, тобто залишається 16 гіперкуба. На наступних кроках ми пророблюємо такі самі дії з кожним гіперкубом що залишився. Після нескінченної кількості кроків ми отримаємо чотиривимірний пил Кантора (див. рис.3.11).

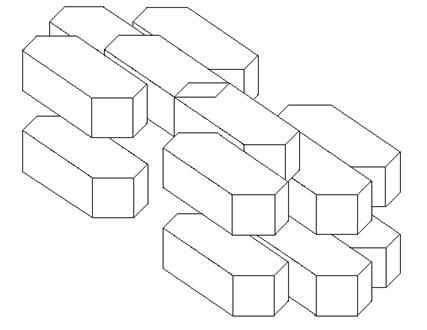
Рис. 3.11.

Аналітичний спосіб задання. Для того щоб аналітично задати чотиривимірний пил Кантора будемо й надалі використовувати точки в трійковій системі числення виду (для 4-х вимірного простору):

,

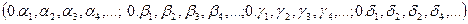де .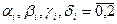

Якщо 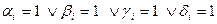, то ми отримаємо чотиривимірний пил Кантора.

Розмірність самоподібності. Порахуємо розмірність чотиривимірного пила Кантора (к=16, m= ).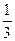

.

Звідки .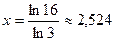

3.5.5. П о р і в н я л ь н а х а р а к т е р и с т и к а. Щоб узагальнити килим Серпінського на n - вимірний простір, насамперед складемо таблицю з результатами побудов (вказується кількість об’єктів, що залишаються) кожного об’єкта які розглядали в 1-х, 2-х, 3-х, 4-х вимірних просторах.

n=1 1

n=2 1 5

n=3 1 7 19

n=4 1 9 33 65

Представивши числа певним чином, ми отримаємо нову таблицю:

n=1 ;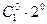

n=2 ; ;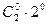

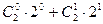n=3 ; ; ;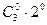

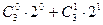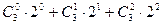n=4 ; ; ; ;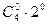

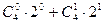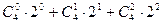Тепер узагальнимо на n- вимірний простір:

n=n-1 ; ; ;… …. ;

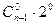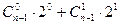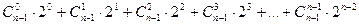n ; ; ;… … .

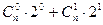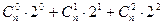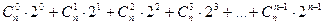Дата добавления: 2015-08-21