Описовий спосіб задання. Цю фігуру можемо отримати так: візьмемо квадрат, на першому кроці поділимо його на 9 конгруентних квадратиків і відкинемо середній квадратик, залишивши його сторони. На наступному кроці проробимо це з кожним квадратиком, що залишився і т.д. В границі ми отримаємо деяку фігуру –килим Серпінського (див. рис. 3.1).
Рис. 3.1.
Аналітичний спосіб задання. Для того, щоб аналітично задати килим Серпінського, а також його узагальнення на 3-х та 4-хвимірні простори, будемо використовувати точки в трійковій системі числення виду (для 2-х вимірного простору): 
, де 
.
Якщо 
, , то ми отримаємо килим Серпінського.
По-іншому аналітично килим Серпінського можна задати так: позначимо множину його точок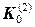 
(верхній індекс позначає розмірність простору, якому належать точки досліджуваної множини, нижній – будову елементів, які викидаємо, наприклад, якщо викидаємо сфери – індекс нуль, циліндри – одиниця, площини – двійка і т.д.), тоді
.
Розмірність самоподібності. Порахуємо розмірністькилима. Викорстуовуючи означення розмірності само подібності розв’яжемо рівняння
,
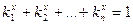де 
– коефіцієнти подібності.
На першому етапі побудови ми ділимо квадрат на 9 квадратиків, і викидаємо 1, отже таких доданків буде 8 (к = 8), а коефіцієнт само подібності рівний 
(m= ). Підставивше дані в рівняння, одержимо:
.
Звідки 
.
Отже, розмірність самоподібності килима Серпінського x» 1,893.
Площа. Порахуємо площу килима Серпінського. Для цього порахуємо площу тих квадратів, що викидались в процесі побудови. Якщо площа початкового квадрата була рівна 1, то площа квадратів, що викидаються буде:
.
Тобто площа килима Серпінського дорівнює нулю.
Дата добавления: 2015-08-21; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Завдання | | | Ц в и н т а р С е р п і н с ь к о г о |