Узагальнення серветки Серпінського

Розглянемо фрактальну множину 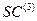, яка є просторовим аналогом трикутного килима Серпінського.

3.7.1. О п и с о в и й с п о с і б з а д а н н я. На першому кроці побудуємо чотири площини, кожна з яких паралельна одній з граней правильного тетраедра і проходить через середини трьох ребер, що виходять з вершини, протилежної цій грані. Утворений октаедр викинемо з початкового тетраедра і отримаємо чотири конгруентні правильні тетраедри. На другому кроці з ними виконуємо такі ж дії і так далі до нескінченності. Деяке уявлення про цю фігуру дає рис. 3.20.

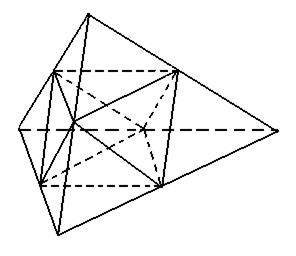
Рис. 3.20.

Утворений фрактал (рис. 3.21) Б.Мандельброт називає фрактальною павутиною [12,ст. 207].

Рис. 3.21. Фрактальна павутина

Фрактальна розмірність павутини 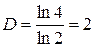. Хоч розмірність і ціле число, але менше за топологічну розмірність об’єкта. Аналітичний спосіб задання цього фрактала:

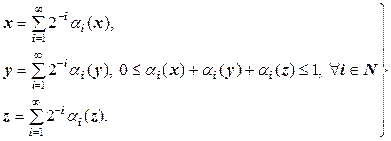
Якщо ж, так як і в двовимірному випадку видалятимемо лише один верхній кубик, який лежить навпроти початку осей координат, отримаємо теж об’єкт з фрактальними властивостями. Його фрактальна розмірність

.

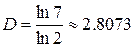Аналітично цей фрактал задається так:

Цей об’єкт з точки зору теорії розгалужень по своїй структурі ближчий до фрактальної піни. Деяке уявлення про нього можна отримати з рис.3.22, на якому показано ті кубики, які викидаються на перших декількох етапах побудови.

Рис. 3.22.

Отже, як і у випадку килима Серпінського, на основі аналізу отриманих фракталів, бачимо певну схему. Слідуючи у простори вищих порядків, отримуватимемо нові й нові фрактальні множини, зовнішній вигляд яких ще не було зображено.

3.7.2. А н а л і т и ч н и й с п о с і б з а д а н н я. Нехай - множина, утворена на -му кроці побудови множини .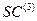

Дата добавления: 2015-08-21