Приклад 9. Побудова системи одночасних структурних рівнянь

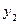Розглянемо модель з двох регресій, одна з яких характеризує величину експорту товарів , а друга – імпорту (в ум. гр. од.). В якості попередньо визначених змінних (екзогенних величин) розглянемо національних дохід та середній обіг зовнішньої торгівлі країн блоку СНД :

Таблиця 10.1. Вихідні дані задачі

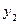
	5,5
	6,1
	6,9
	7,4
	7,9
	8,3
	8,8
	9,1
	9,8
	10,2

За даними спостереження побудувати за допомогою ННК та 2МНК модель на основі одночасних структурних рівнянь, яка характеризує стан зовнішньої торгівлі країни.

Розв’язання

Для кожного рівняння перевіримо умову порядку:

Функція експорту: рівняння точно ототожнене.

Функція імпорту: 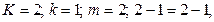рівняння точно ототожнене.

Таким чином, в даній моделі ми маємо змогу знайти оцінки параметрів обох рівнянь за допомогою ННК чи застосувавши 2МНК.

Запишемо скорочену форму даної системи рівнянь:

Параметри визначених регресій знайдемо за допомогою МНК. В результаті скорочена форма структурної моделі матиме вигляд:

Виконаємо необхідні розрахунки для оцінки коефіцієнтів детермінації та фактичних значень критерію Фішера для отриманих регресійних рівнянь.

Таблиця 10.1. Розрахункові дані задачі

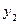
		52,59	75,56	2025,00	1444,00	2247,25	1255,96
		64,31	84,05	1369,00	625,00	1273,95	726,16
		72,10	95,69	841,00	289,00	778,59	234,51
		79,90	102,84	400,00	64,00	403,99	66,57
		91,06	109,86	49,00	0,00	79,94	1,29
		105,02	115,28	9,00	36,00	25,18	18,31
		119,53	122,17	289,00	121,00	381,45	124,71
		127,90	126,31	784,00	361,00	778,59	234,51
		138,49	136,34	1521,00	576,00	1481,70	642,28
		149,10	141,89	2601,00	784,00	2410,51	954,42
		Сума	9888,00	4300,00	9861,16	4258,73

Для заданого рівня значимості та і ступенів свободи фактичні значення критерію Фішера значно перевищують його критичне значення, тобто побудовані регресії є адекватними зі ймовірністю 0,95.

Знаходимо оцінки параметрів структурної моделі за ННК.

За формулами:

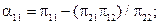
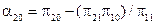
обчислюємо: ; ; ; ; ; .

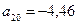Таким чином:

Знаходимо оцінки параметрів структурної моделі за 2МНК.

Використовуючи оцінені значення ендогенних змінних і (в таблиці) та дані спостереження за змінними і і застосовуючи МНК другий раз знаходимо оцінки структурних параметрів. В результаті:

Два різні методи побудови моделей на основі одночасних структурних рівнянь дозволили отримати однакові результати. При цьому ННК був застосований, оскільки обидва рівняння системи точно ототожнені, а даний метод створений для оцінки параметрів точно ототожнених рівнянь. 2МНК був створений для оцінки параметрів переототожнених рівнянь моделі, проте його властивості дозволяють використовувати цей метод для оцінки параметрів в тому числі точно ототожнених рівнянь. На прикладі ми переконалися, що отримані оцінки справді однакові.

Дата добавления: 2015-10-23