Рангова умова ототожнення

Умова порядку, яка обговорювалась раніше, є обов’язковою, але не дос­татньою умовою ототожнення. Тобто може статися так, що навіть якщо умова порядку виконана, рівняння може бути неототожненим, тому що попередньо визначені змінні, які опущено в ньому, але є в моделі, можуть бути залежними. Через це відповідність між структурни­ми коефіцієнтами (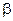) і коефіцієнтами скороченої форми (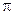) не зберігаєть­ся. Тобто ми не можемо оцінити структурні параметри за коефіцієнтами скороченої форми. Тому потрібно мати як достатню, так і необхідну умову ототожнення. Такою умовою є рангова умова ототожнення, яка форму­люється таким чином.

Рангова умова ототожнення: в симультативній моделі, яка містить рівнянь з ендогенними змінними, рівняння буде ототожненим тоді і тільки тоді, коли ранг матриці, утвореної з коефіцієнтів, котрі відповідають опущеним змінним рівняння, що розглядається, у всіх інших рівняннях моделі, крім даного, дорівнює .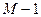

Алгоритм перевірки рівняння за ранговою умовою:

1. Записати систему симультативних рівнянь у табличній формі.

2. Викреслити коефіцієнти рядка, в якому з’являється рівняння, що розглядається.

3. Викреслити стовпці, відповідні ненульовим коефіцієнтам, рівняння, що розглядається.

4. Отримаємо необхідну матрицю. Якщо ранг матриці точно дорівнює 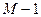, то рівняння ототожнене. Якщо ранг матриці менший, ніж 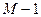, рівняння неототожнене.

На базі умов порядку та рангу можна сформулювати загальні принципи ототожнення структурного рівняння в моделі, яка складається з симультативних рівнянь.

1. Якщо > 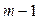і ранг матриці буде дорівнювати 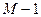, то відповідне рівняння переототожнене.

2. Якщо = 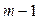і ранг матриці буде дорівнювати 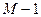, то відповідне рівняння точно ототожнене.

3. Якщо ≥ 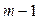і ранг матриці буде меншим, ніж 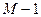, то відповідне рівняння неототожнене.

4. Якщо < 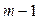і ранг матриці буде меншим, ніж М-1, то відповідне рівняння неототожнене.

Дата добавления: 2015-10-23