Основні правила ототожнення

Розглянемо основні правила ототожнення симультативних моделей. Введемо таку систему позначень:

- кількість ендогенних змінних у симультативній моделі;

- кількість ендогенних змінних у окремому рівнянні;

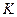- кількість попередньо визначених змінних у моделі;

- кількість попередньо визначених змінних у окремому рівнянні.

З врахуванням введеної системи позначень сформулюємо обов’язкову (але не достатню) умову ототожнення, яка має назву «умова порядку» і може бути визначена двома різними, але еквівалентними способами.

Визначення 1. Для ототожнення рівняння в ньому має бути опущено щонайменше 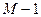змінних, які з’являються в цілому в моделі. Якщо опущено рівно 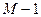змінних, рівняння буде ототожненим. Якщо опущено більше, ніж 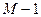змінних, воно буде переототожненим.

Визначення 2. Для ототожнення рівняння число попередньо визначених змінних, опущених в ньому, має бути не меншим за число включених в нього ендогенних змінних мінус одиниця, тобто

Якщо , рівняння точно ототожнене, але якщо > , воно переототожнене.

Щоб проілюструвати умову порядку, звернемось до попередніх прикладів.

Приклад 1

Функція попиту:

Функція пропозиції:

– ціна. Ця модель має дві ендогенні змінні та і жодної попередньо визначе­ної. Для ототожнення в кожному рівнянні має бути опущена щонайменше змінна. В даному разі жодне з рівнянь не буде ототожне­ним.

Приклад 2

Функція попиту:

Функція пропозиції:

У даній моделі і – ендогенні, а – екзогенна.

Застосовуючи умову порядку, бачимо, що функція попиту неототожнена. З іншого боку, функція пропозиції ототожнена, бо в ній опущено рівно одну змінну ().

Приклад 3

Функція попиту:

Функція пропозиції:

У даній моделі і – ендогенні, а і – екзогенні змінні. У першому рівнянні опущено рівно одну змінну , у другому рівнянні також опуще­но рівно одну змінну . Кожне рівняння може бути ототожнене за умо­вою порядку, а отже, і модель в цілому також може бути ототожненою.

Приклад 4

Функція попиту: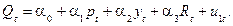

Функція пропозиції: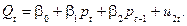

У даній моделі і – ендогенні, а , і – екзогенні змінні. У функції попиту опущено рівно одну змінну , за умовою порядку вона точно ототожнена. А у функції пропозиції опущено дві змінні та , отже, вона переототожнена. Як зазначалось раніше, в даному разі є два способи оцінки .

Як показують попередні приклади, ототожнення рівнянь симультатив­них моделей можливе тоді, коли в окремих рівняннях опущено одну чи більше змінних, які є ще де-небудь у моделі.

Дата добавления: 2015-10-23