Тиімді кодтау туралы түсінік

Жоғарыда айтылғандай, хабарламаның белгілемелері екілік символдардың қатарына ауысып отырады. Қарастырылған құрылғыларда бұл ауысым келіп түскен хабарламалардың статистикалық қасиетін есепке алмай орындалды.

Хабарлама көзінің статистикалық қасиеттерін есепке алсақ, хабарламаның бірлік белгісі үшін қолданылатын символдардың орташа мәнін азайтуға болады. Бұл үрдіс шу болмаса, хабарламаның беріліс уақыты немесе сақтағыш құрылғының көлемін азайтуға үлес қосады.

2. Шеннонның канал кедергісіз арна үшін кодтаудың негізгі теоремасы.

Хабарламаны дискретті канал арқылы кедергісіз әрі тиімді кодтау Шеннонның теоремасына негізделген, ал бұл теореманы келесідей тұжырымдауға болады:

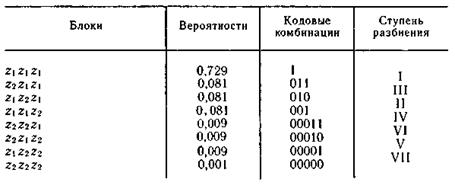
1.Хабарлама көзінің кез-келген өндірістік қабілетінде, арнаның ең аз жіберілім қабілеті кезінде, яғни

Бұл жердегі ε – кез-келген шамадағы оң, әрі аз шама, хабарлама көзі арқылы кез-келген хабарламаны жібере алатын кодтаудың тәсілі бар екені айтылады.

2. Егер 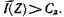болса, хабарламаның шексіз жинақталуын қамтамасыз ететін кодтау тәсілі болмайды. Дәлелдеме негізінде арнандағы хабарламалардың кодтау кезіндегі символдар реттілігін жеке белгі емес, оның асимптоталық теңгерілген ықтималдығы теоремасы орындалатындай ұзындықтағы хабарламаның жылдамдығын арттыру ойы жатыр. Бұл жағдайда, ең алдымен, қарапайым тізбектер кодталады.

Егер кодталатын реттіліктегі белгілердің саны Ν-ге тең болса, ал хабарлама көзінің энтропиясы Η(Ζ)-ға тең болса, онда (10.1)-ші формулаға сәйкес қарапайым реттіліктердің саны мынаған тең:

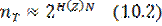
Ν = Τ/τ, бұл жердегі Т — кодталатын реттіліктің ұзындығы, τ – бір белгі ұзындығы, онда:

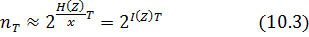
Әрбір қарапайым реттілікке М алфабитіндегі көлемдегі Т жалғастырылған уақыттағы сәйкес кодтық комбинация қою керек. V_T амал (манипуляция) жылдамдығы кезінде кодтық комбинациядағы симводар саны TV_Т –ға тең болады, ал ол, өз кезегінде, n_kтүрлі кодтық комбинация құруға мүмкіндік береді:

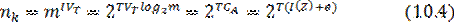
(10.3) және (10.4)-ші теңдеуді салыстыра отырсақ, 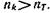екеніне көзіміз жетеді. Егер 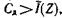болса, арна арқылы жіберілетін кодтық комбинациялар саны барлық қарапайым тізбектілікті кодтау үшін жетеді, тіпті артық қалады.

Қарапайым емес реттіліке негізінен символдардың үлкен баршылығы бар кодтау сәйкестендіріледі. Бұл комбинацияларды ажырату үшін бастапқы және ақтық кодтық комбинациялар қолданылады. Бірақ барлық қарапайым емес реттіліктерге бір кодтық комбинацияны қоюға болады.

Егер 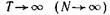болса, қарапайым емес реттіліктің пайда болу ықтималдығы нөлге қарай ұмтылады, бұл бірінші мысалға ешқалай әсер етпейді, ал екіншісіне –сенімділік деңгейінде байқалады.

Егер қарапайым, теңгерілген ықтималды реттілікті кодтау аясында қалсақ, біз арнамызға символдардың арна кірісіне теңгерілген әрі тәуелсіз артықшылықсыз келіп түсуін қамтамасыз етеміз.

Теореманың екінші бөлігінің растығы - 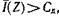болған кездегі берілістің мүмкін емес екендігін көрсетеді. Бұл берілген класстағы көптеген хабарлама көздерінен алынған арнадағы максималды жылдамдықтағы хабарламаның берілуінен алынған. Сондықтан арнаның берілу қабілеті оның өндірістік қабілетінен жоғары болса, хабарлама беретін жақтағы хабарлама жиынтығының болуын сиппаттайды.

Шеннонның теоремасының тағы бір сипатталуы: хабарлама көзінен келіп түскен Η(Ζ) энтропиясы бар хабарламаны m алфабитті көлем арқылы келесідей кодтауға болады; l _cр хабарламаның бірлік белгісіне келетін символдардың орташа мәні 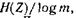мәніне жақындайды, бірақ ол бола алмайды.

Берілген ұйғарым да теңгерілген ықтималды реттілікті кодтау аясында, арнаға символдардың арна кірісіне теңгерілген әрі тәуелсіз келіп түсу дәлелдемесі арқылы түсіндіріледі, яғни әрбір белгідегі ақпараттың максималды көлемі log m-ге тең болады. Жоғарыда айтылғандай, біздің жағдайда кодтау ұзын блоктар арқылы жүзеге асса онда берілген ұйғарымның растығы анықталады.

Дербес жағдайда, яғни екілік кодтауда (m = 2) хабарлама бірлігіне сәйкес келетін символдардың ортақ саны оның энтропиясы деңгейіне деңгейіне дейін түсіп кетуі мүмкін, ал ол келесі өрнекпен анықталады: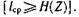

Коррелляциясыз тізбекті белгілерді тиімді кодтау әдісі

Теорема кодтау әдісінің нақтылығын көрсетпейді, бірақ кодтық комбинациядан символ таңдағанда ол максималды ақпарат әкелетінін таңдауға тырысу қажет.

Соған сәйкес, әрбір символ 0 және 1 сандарын қамтиды, және әрбір таңдау алдыңғы мәндеріне тәуелді болмауы керек.

Статистикалық ара-қатынастың болмағандығы үшін белгілердің арасында тиімді кодтау әдістерін тұңғыш рет Американың ғалымдары Шеннон және Фано ашты.

Оның әдістемелері байыпты әрі ажыратылмайды, соған сәйкес код Шеннон - Фано код атауын алды.Код келесідей үлгімен құрастырылады: алфавит белгілерін кестеден мүмкіндік бойынша кему ретімен жазып шығады. Одан кейін оларды 2 группаға бөледі, әрбір группада ұқсас мүмкін суммалар жинақталады. Жоғары бөлігіндегі барлық мәндерге бірінші символ ретінде 0 жазылады, ал төмендегілерге - 1. Әр группадан алынған мәндерді бірдей мүмкін суммалармен тағы екі топшаларға бөледі және т.с.с. Процесс әрбір топшада бір-бір белгіден қалғанша қайталана береді.

Мысал 5.5. 5.4 кестесінде көрсетілгендей, сегіз белгіден құралған тиімді кодтау жүргіземіз.

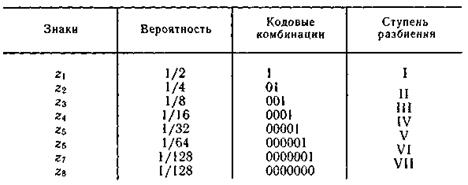
Қалыпты жағдайдағы кодтауда әрбәр белгіні таныстыру үшін 3 екілік символдар қажет болады.Шеннон-Фано әдістемесін пайдаланып, 5.4 кестеде келтірілген кодтық комбинацияны аламыз.

Себебі белгінің мүмкіндіктері собой екіліктіңцелочисленные жағымсыз дәрежелерін ұсынады, солартығым при кодтау толықтай серпійді. Символдың орташа мәні энтропия мәніне тең болады. Осыған тоқталайық:

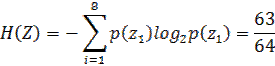
және символдардың орташа мәні белгіге

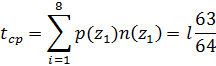
Көбіне алфавит үшін сегіз белгі символының орташа саны бегіден 3 есе аз, бірақ энтропиядан көп Η(Ζ).

Мысал 5.6. 5.5 кестесінде көрсетілгендей тиімді кодтауда кодтық комбинацияның орташа ұзындығын анықтаймыз.

Ансамбль энтропиясы 2,76-ға тең. Шеннон - Фано әдісі бойынша ансамбльдің жеке таңбаларын кодтық комбинацияларға салыстырулар нәтижесінде 2,84 таңбасына тең символдардың орташа санын аламыз.

Кесте

Демек, символдардың тізбектелуінде кейбір артықшылықтар қалды. Шеннон теоремасында бұл артықшылықты сонымен бірге егер жеткілікті үлкен блоктарға кодтауға өтсе, шеттетуге болады.

Мысал 5.7

Пайда болу ықтималдықтары р (z1) = 0, 9 және ρ (z2) = 0, 1 болатын әліпби көмегімен құрастырылған z1 және z2 таңбаларынан тұратын хабарламалардың тиімді кодтау процедурасын қарастырамыз.

Ықтималдықтар тең емес болғандықтан, осындай әріптер бойынша тізбектелу артықшылыққа ие болады. Бірақ әріп бойынша кодтауда біз ешқандай әсер алмаймыз.

Шындығында, энтропия 0, 47-ге тең уақытта, әрбір әріптің берілуі үшін 1 немесе 0 символы керек.

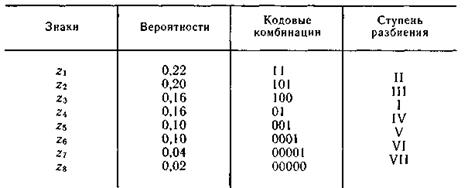
Екі әріпі болатын блоктарды кодтауда, 5.6. кестесінде көрсетілген кодтарды аламыз.

Кесте

Таңбалар статистикалық байланыссыз болғандықтан, блоктардың ықтималдықтары, оны құрайтын таңбалардың ықтималдықтарының туындысымен анықталады.

Блок үшін символдардың орташа саны 1, 29-ға, ал әріп үшін — 0, 645-ке тең.

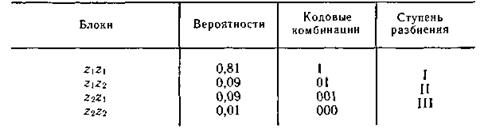
Үш таңбадан тұратын блокдарды кодтау үлкен әсер береді. Сәйкесінше ансамбль мен кодтар 5.7. кестесінде берілген.

Кесте

Блок үшін символдардың орташа саны 1,59-ға тең, ал таңба үшін — 0, 53-ке, энтропиядан небәрі 12 % -ға артық. Теориялық минимум Η (Ζ) = 0, 47 таңбалардың шексіз санынан тұратын блоктарды кодтауда жетуі мүмкін:

Біздің тарапымыздан түзетілмеген таңбасы бар әліпбилер қаралғандықтан, блоктарды ірілендіруде кодтау тиімділіктерінің үлкеюі өте алыс статистикалық байланыс есебіне қатысты емес екенін айта кеткен шарт.Тиімділікті жоғарылату, блоктарды ірілендіруде пайда болатын ықтималдықтардың жиынын, өте жақын орналасқан жиынтық ықтималдықтар бойынша шағын топтарға бөлуге болатындығымен анықталады.

Кесте

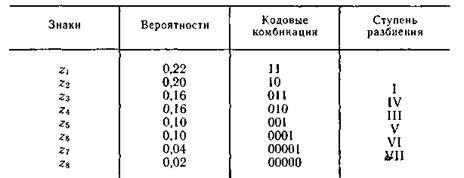
Шеннон— Фаноның қарастырылған әдістемесі кодты әрдайым бірмәнді құрастыруға алып келмейді. Анығында шағын топтарға үлкен ықтималдық бойынша бөліктеуде жоғарғы сияқты төменгі шағын топтарға да жасауға болады. Мысалы, ықтималдықтардың жиыны 5.5 кестесінде келтірген, оны 5.8 кетесінде көрсетілгендей бөліктеуге де болар еді.

Көрсетілген кемшіліктен Хаффмена әдістемесі бос. Ол әріпке символдыңең кіші орташа санымен берілген ықтималдықтарды бөлу үшін кодтың бірмәнді құрастырылуына кепілдік береді.

Екілік код үшін әдістеме келесідей болады. Хабарлама әліпбинің әріптері ықтималдықтардың кему ретімен негізгі бағанаға жазылады. Екі соңғы әріп жиынтық ықтималдық жазатын бір қосалқы әріпке біріктіреді. Біріктіруге қатыспаған әріптердің ықтималдықтары мен алынған жиынтық ықтималдық қосымша бағанада ықтималдықтардың кему ретімен қайтадан орналасады, ал екі соңғысы біріктіріледі. Процесс ықтималдығы бірлікке тең жалғыз қосалқы әріпталғанша созылады.

Мысал 5.8

Хаффман әдістемесін қолдану арқылы 5.5 кестесінде келтірген таңбалар ансамблінің тиімді кодтауын іске асырамыз.

Кодтаулар процессі 5.9 кестесінде түсіндіріледі. Осы таңбаға лайықты кодтық комбинацияларды құрастыруға таңбаның кесте жолдары мен бағандары бойынша өтетін жолын бақылау қажет.

Кесте

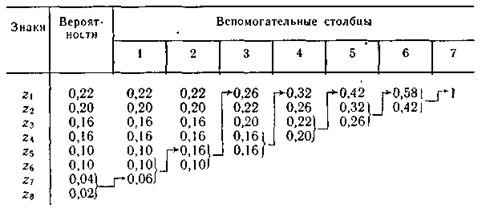
Көрнекілік үшін кодтық ағаш тұрғызамыз. Ықтималдығы 1-ге тең нүктеден, екі тармақ бағыттаймыз, үлкен ықтималдықты тармаққа 1 символын жазамыз, ал кішісіне 0. Осындай тізбектей тармақталуды әрбір әріптің ықтималдығына жеткенше дейін жалғастырамыз. Әріптер әліпбиі үшін кодтық ағаш 5.9 кестесінде, және 5.16 суретінде берілген.

Енді, кодтық ағаш бойынша жоғарыдан төмен қозғала отырып, әрбір әріп үшін оған лайықты кодтық комбинацияны жазып алуға болады:

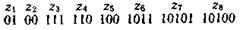
Тиімді кодтардың префиксті талабы. Тиімді кодтардың құрастырылу әдістерін қарап шығып, көп ықтимал таңбамен ұзынырақ, ал аз ықтимал таңбамен қысқа кодтық комбинацияларды иемдену арқылы болып жатқанына көз жеткізу қиын емес. Осылайша әсер кодтық комбинациялардағы символдар санының айырмашылығымен байланысты. Ал бұл қайта кодтауда қиындықтарға алып келеді. Кодтық комбинацияларды ажырату үшін арнайы бөлгіш символ қоюға болады, бірақ кодтық комбинациялардың орташа ұзындығы символға үлкейгендіктен, біз жеткен әсер едәуір төмендейді.

Қосымша символдарды енгізусіз бірмәнді қайта кодтауды қамтамасыз етуге болады. Ол үшін бір де бір код комбинациясы бастапқы ұзын комбинациямен дәл келмейтін тиімді кодты тұрғызу қажет. Бұл шартты қанағаттандыратын кодтар, префиксті кодтар деп аталады. Префиксті 100000110110110100 код комбинацияларының тізбегі

Кодмысалы

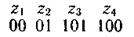
Қайта кодталады: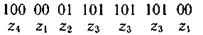

Префиксті 000101010101 код комбинацияларының тізбегі

Код мысалы

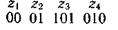
(01 комбинациясы 010 комбинацияның бастауы болып табылады) қайта кодтау әртүрлі болуы мүмкін:

Немесе

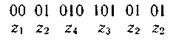
Шеннона – Фано немесе Хаффмен методикаларын қолдана отырып алған кодымыз префиксті код екеніне көзіміз жетті.

Белгілердің коррелироенген тізбегін тиімді әдіспен кодтау. Декорреляция шығыс тізбегінің алфавит таңбаларымен ірілетуге болады. Бастауыш хабарлама беруші 2-3 немесе n знакты үйлестіруші болады:

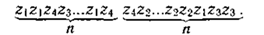
Әр үйлестіруші Шеннона — Фано немесе Хаффмен әдістері бойынша қойылады.

Мұндай әдістердің жетіспеушіліктерінің бірі, бірінен соң бірі кіріс үйлестірушілерінің корреляциондық байланыс арасында есептелмейді. Сонымен әр үйлестіруші ге қанша көп таңба кірсе, сонша аз көрсетеді.

Көрсетілген жетіспеушілікті диаграмм, триграмм немесе l -грамм кодтау әдісі бойынша шешуге болады. Шарт бойынша l-граммалы үйлестіруші l шектес таңбаны хабарлайды. Екі шектес таңбалы үйлестірушіні диаграмма, үш шектес таңбаны триграмма т.с.с.

Енді кодалау үрдісінде l -грамма хабарлама бойынша шексіз орналасып отырады

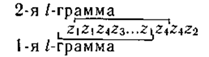
Әрбір келесі таңбаның кодтық мәні l -1 алдындағы таңбаға байланысты және Шеннона - Фано или Хаффмен әдісінің әр түрлі l -граммдық мүмкіндіктері арқылы табылады.

l- дің нақты мәнін корреляция байланысының таңбалар немесе техникалық реалиязияның кодтау және декодтау құрылғылары арқылы таңдайды.

Тиімді кодалау жүйесінің жетіспешіліктері. Жетіспеушіліктің бір себебі кодты комбинацияның ұзындығының әр түрлілігінде. Егер хабарлама көзі шешімі кезінде басқарылмайтын болса, кодталған құрылғы бірдей уақыт өткен соң әр түрлі ұзындықты комбинация корсетеді. Себебі байланыс сызығы тиімді болған кезде ғана қолданылады, қашан символдар оған түпкілікті жылдамдықпен кіргенде, кодталған құрылғы шығысында буферлі құрылғы болуы қажет. Ол кіріс символдарын жинап түпкілікті жылдамдықпен байланыс сызығы жібереді. Аналогты құрылғы қабылдау жағынада қажет.

Екінші жетіспеушідік ақпарат беру кідірісімен байланысты.

Ең үлкен әсер ұзын блокты кодтағанда пайда болады, бұл таңбаларды жинауға әкеледі, алдын ала сәйкес келетін тізбектілік символдар қоярда. Декодтағанда кідіріс қайта пайда болады. Жалпы кідіріс уақыты үлкен болуы мүмкін, әдетте блок пайда болған кезде. Мұны кодтау блогының ұзындығын таңдаған кезде ескерген жөн.

Тағы бір жетіспеушілік спецификалық анық жету кедергісінің әсері. Бірлік қателік беріліп жатқан кодтық комбинацияны өзіне сәйкес емес кодтық комбинацияға жіберуі мүмкін. Оның әсері дұрыс емес декодталған қатар комбинациясына алып келеді, ол қате тегі деп аталады.

Арнайы тиімді кодтың құрылысының әдістерімен қате тегі минимумға әкелуге тырысады.

Бақылау сұрақтары:

1. Тиімді кодалаудың ұғымы

2. Шеннон теоремасы

3. Белгінің корреляционды емес тізбектілігінің тиімді кодалауының әдістері.

4. Хаффмен әдісі

Дата добавления: 2015-10-23