Дифференциалдық энтропия

Практикада ақпарат көздерінің мүмкін күйлерінің көбісі континиум құрайды, яғни ақпарат көздері үздіксіз.

Үздіксіз ақпарат көзінің энтрпаиясын келесі түрде анықтаймыз:үздіксіз кездейсоқ шаманың өзгеру дипазонын бөлейік U, п соңғы шамасыCu аз интервалында. Cu аз болғандықтан, р (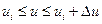) ықтималдық реализациясы u мәні u_i, u_i+Cu интервалында:

p()=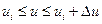

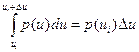
Дискретті кездейсоқ шама U энтрапиясы мына түрде беріледі:

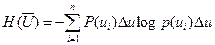
немесе

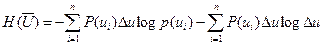
Өйткені

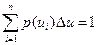
онда

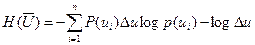
Кемуіне байланысты 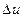р (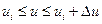), нөлге жақын р(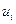) ықтималдыққа жақындайды, U дискретті шамасының көлемі - U үздіксіз кездейсоқ шамасына жақындайды.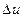 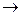0 шекке жеткенде үздіксіз энтропия көзі H(U) үшін келесі теңдікті аламыз:

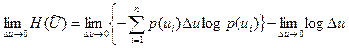
немесе

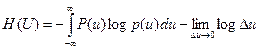(3.4)

Бұл шама 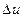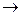0шексіздікке ұмтылады,толығымен анықтамаға сәйкес келеді, шексіз үлкен саннан тұратын таңдаудың анықталмағандығы шексіз үлкен болады.

(3.4)қатынасының оң бөлігінің бірінші мүшесі-соңғы мағынасы,U –дың шексіз мүмкін үлкендігін бөлу заңына тәуелді және U кванттау қадамына тәуелсіз.

Осы қатынастың екінші мүшесі U мүмкін үлкендігінің кванттау қадамына ғана тәуелді,H(U)осыдан шексіздікке айналады.

Үздіксіз көзінің ақпараттық ерекшеліктерінің соңғы сипаттамасын алудың бір жолы үздіксіз көзінің анықталмағандығының сапасы ретінде(3.4) қатынасының бірінші мүшесі алынады:

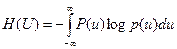(3.5)

Ол қатыстық дифференциалды энтропия немесе жай үздіксіз ақпарат көзінің дифференциалдық энтропиясы деп аталды. Дифференциалдық энтропия ерекшелігі:

a. Егер U –ң мүмкін өлшемінің жалғыз шектеуі оның мүмкін мәндер аймағы болса,онда максималды дифференциалдық энтропия осы аймақтағы мүмкіндікті тең бөлуге ие.

б. Егер U үздіксіз мүмкін өлшемі аймағының шектеуі жоқ болса,бірақ белгілі,дисперсиясы шектеулі,максималды дифференциалдық энтропиясы U өлшемінің дұрыс бөлісуіне ие.

Негізгі әдебиеттер:2[111-119J; 3(109-114]; 9J44-46].

Бақылау сұрақтары:

1.Ақпарат саны және энтропиясы бір-бірімен қалай байланысты?

2. Асқын мағынасын анықтаңыз.

3. к тең емес ықтималды белгілерден тұратын хабарламадағы ақпарат санын анықтаңыз.

4. Дифференциалды энтропияға анықтама беріңіз және оның ерекшеліктерін сипаттаңыз.

Дата добавления: 2015-10-23