
Читайте также:
|
Биологические системы состоят из огромного числа частиц (молекулы, атомы, ионы). Поведение таких систем подчиняется законам теории вероятностей и статистической термодинамики. В последней термодинамические величины в равновесном состоянии получаются как средние от некоторых функций координат и импульсов частиц. При исследовании большого количества частиц указывают относительное время пребывания системы в данном состоянии и рассматривают это время как меру вероятности. Движение системы от менее вероятных состояний к более вероятным отвечает, с термодинамической точки зрения, росту энтропии и является необратимым. Связь энтропии с термодинамической вероятностью выражается уравнением Больцмана:
 , ,
| (1.29) |
где  - постоянная Больцмана;
- постоянная Больцмана;
 - термодинамическая вероятность (число микросостояний, реализующих данное макросостояние).
- термодинамическая вероятность (число микросостояний, реализующих данное макросостояние).
Для неизолированных систем общее изменение энтропии равно сумме изменения энтропии системы и энтропии окружающей cреды:
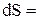  сист + сист +  окр. ср. окр. ср.
| (1.30) |
Поэтому, для изолированных систем удобнее пользоваться другими критериями самопроизвольности процессов и равновесия, которые были предложены Гиббсом.
Запишем фундаментальное уравнение, объединяющее первый и второй законы термодинамики:

| (1.31) |
При условии постоянства объема и температуры V, T=const уравнение (1.31) примет вид
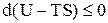 , ,
| (1.32) | |
Обозначим  , ,
| (1.33) |
где F - функция Гельмгольца (иногда энергия Гельмгольца), изохорно-изотермический потенциал или просто изохорный потенциал.
Из уравнений (1.32) и (1.33) следует:
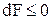 . .
| (1.34) |
Знак < относится к самопроизвольному процессу, знак = - к равновесному. Таким образом, в изохорно-изотермических условиях, протекание самопроизвольного процесса сопровождается уменьшением функции Гельмгольца; при равновесии она принимает постоянное и минимальное значение:
| dF = 0; d2F > 0 |
При постоянстве давления и температуры, P, T=const уравнение (1.31) можно записать в виде
 . .
| (1.35) |
Выражение в скобках называется функцией Гиббса (энергией Гиббса) или изобарно-изотермический потенциал:
 . .
| (1.36) |
Отсюда следует, что
 . .
| (1.37) |
Таким образом, в системе, находящейся при постоянных температуре и давлении, самопроизвольно могут протекать процессы, которые сопровождаются уменьшением функции Гиббса, причем пределом их протекания, т. е. условием равновесия, служит достижение некоторого минимального для данных условий значения функции Гиббса (dG<0 в самопроизвольном процессе; dG=0; 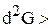 0- при равновесии). Следовательно, изменение функций Гиббсаи
0- при равновесии). Следовательно, изменение функций Гиббсаи
функции Гельмгоца (DF, DG) позволяет решить вопрос о направлении самопроизвольного процесса при постоянных объеме и температуре или постоянных давлении и температуре.
Функция Гиббса в химии и биологии используется чаще, чем функция Гельмгольца. Это связано с тем, что химические и биологические процессы протекают, как правило, в условиях, когда система находится при постоянном давлении, но не при постоянном объеме.
Поскольку  , необходимо учитывать вклад энтальпийного
, необходимо учитывать вклад энтальпийного  и энтропийного
и энтропийного  факторов в величину и знак
факторов в величину и знак  .
.
Вклад энтальпийного (DH) и энтропийного (TDS) членов
в знак и величину изобарно-изотермического потенциала (DG)
DG = DH - TDS
| Знак DH | Знак DS | Знак DG | Направление протекания реакции |
| 1. “-“ реакция экзотермическая | “+“ возрастание энтропии | “-“ | Реакция термодинамически возможна и протекает самопроизвольно в прямом направлении при любых температурах |
| 2. “-“ реакция экзотермическая | “-“ убывание энтропии | “-“ если |DH| > |TDS| | Реакция термодинамически возможна и протекает при низких температурах |
| 3. “+“ реакция эндотермическая | “+“ возрастание энтропии | “-“ если |DH| < |TDS| | Реакция термодинамически возможна и протекает при высоких температурах |
| 4. “+“ реакция эндотермическая | “-“ убывание энтропии | “+” | Реакция термодинамически невозможна при любых температурах, т. е. протекает в обратном направлении |
Дата добавления: 2015-10-31; просмотров: 153 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тема 1. ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ ХИМИЧЕСКОЕ РАВНОВЕСИЕ. | | | ХИМИЧЕСКОЕ РАВНОВЕСИЕ |