Химическое равновесие

Известно, что многие химические реакции не доходят до конца, т. е. исходные вещества не расходуются полностью на образование продуктов реакции. В этом случае система находится в состоянии динамического равновесия, с течением времени при определенных условиях скорость прямой реакции становится равной скорости обратной реакции. При неизменности внешних условий система находится в состоянии равновесия сколь угодно долго, при этом с термодинамической точки зрения соотношение концентраций исходных веществ и продуктов реакции поддерживается постоянным и отвечает минимальному значению свободной энергии Гиббса. Постоянство состава системы может служить признаком, достаточным для констатирования наступления равновесия, лишь для реакций, протекающих сравнительно быстро. Для реакций, протекающих с незначительной скоростью, состав смеси может оставаться постоянным продолжительное время и состояние равновесия оказывается кажущимся. Для установления равновесия необходимо воспользоваться вторым признаком равновесия - признаком его подвижности. Если система, находящаяся в состоянии равновесия, будет выведена из этого состояния под действием внешних факторов (температура, давление), то после прекращения этих воздействий она самопроизвольно должна вернуться в прежнее состояние. Однако, если этого не происходит, то система не достигла еще состояния равновесия. Поэтому состояние химического равновесия характеризуется двумя признаками: постоянством состава при данных внешних условиях и подвижностью. Состав равновесной смеси характеризуется тем, что в ней концентрации исходных веществ и продуктов реакции находятся в определенном соотношении, которое определяется константой равновесия.

Для реакции аА + вВ = еЕ + fF при равновесии скорость прямой реакции равна скорости обратной реакции и константа равновесия (Кс) может быть представлена соотношением:

(2.1)

где С - равновесные мольные концентрации веществ; а, в, с, f - стехиометрические коэффициенты.

Константу равновесия можно выразить через равновесные парциальные давления компонентов системы:

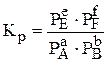
(2.2)

Связь между Кр и Кс описывается уравнением Кр = Кс(RT)Dn.

Учение о химическом равновесии позволяет рассчитывать выход продуктов реакции и раскрывает возможности управления химическими процессами. Следует помнить, что равновесие системы может смещаться при изменении концентрации реагирующих веществ, давления и температуры, константа же равновесия зависит только от температуры. Данная зависимость описывается уравнением изобары (2.3) или изохормы (2.4) Вант-Гоффа:

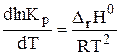
		(2.3)
		(2.4)

где DrН0 - изменение энтальпии, DrU0 - изменение внутренней энергии системы.

Для химических реакций DrН0 и DrU0 соответствуют тепловому эффекту реакций соответственно при р = const и v = const. Знак теплового эффекта определяет зависимость константы равновесия от температуры. Если DrН0 > 0, то реакция эндотермическая, знак производной dlnKp/dT будет положительный, следовательно, с увеличением температуры константа равновесия эндотермической реакции возрастает. При этом равновесие может смещаться в сторону образования продуктов реакции.

Если принять, что тепловой эффект химической реакции не зависит от температуры,то уравнение Вант-Гоффа можно представить в интегральной форме (уравнения 2.5 и 2.6):

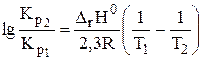
		(2.5)
		(2.6)

где В - постоянная интегрирования.

На основании уравнения (2.6) можно определить тепловой эффект реакции графическим методом, зная константы равновесия при 4 - 5 температурах (рис. 1).

  tg (p - a) tg a = -tg (p - a) = -   D rH0 = 2,3R tg (p - a) =- 2,3R tg a    

Рис. 1. Зависимость lg Kp от обратной температуры.

Для определения направления протекания химической реакции при заданных значениях температуры и давления используют уравнение изотермы химической реакции (2.7):

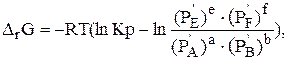
(2.7)

где DrG - изменение изобарно-изотермического потенциала системы при реакции, , , 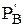, - исходные парциальные давления участников реакции, Кр - константа равновесия, выраженная через равновесные парциальные давления компонентов.

Если DrG реакции < 0, то при данной температуре и заданных исходных парциальных давлениях участников реакции процесс будет протекать самопроизвольно. Если DrG=0, то реакция при этих условиях достигает состояния равновесия. При стандартных условиях, когда исходные парциальные давления равны 1 атм ( = = 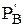= = 1 атм), уравнение изотермы имеет вид:

DrG0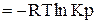

(2.8)

Тогда в общем виде можно записать:

DrG DrG0

(2.9)

Из этого уравнения видно, что если при стандартных условиях DrG0 > 0, то это не свидетельствует о том, что реакция не пойдет. Можно подобрать такое соотношение исходных парциальных давлений и концентраций, при которых DrG станет меньше нуля и реакция будет протекать самопроизвольно.

Дата добавления: 2015-10-31