Тема 1. Основы химической термодинамики химическое равновесие.

Вопросы для семинара 1. Предмет химической термодинамики. Основные термодинамические понятия. Система, фаза, параметры (экстенсивные и интенсивные), состояние системы, процесс. Теплоемкость системы.

Первый закон термодинамики, его формулировки и аналитическое выражение. Энтальпия.

Термохимия. Термохимические уравнения, их особенности и формы записи. Закон Гесса и следствия из него. Стандартное состояние и стандартные условия. Стандартная энтальпия образования и стандартная энтальпия сгорания. Термохимические расчеты и их использование для энергетической характеристики биохимических процессов.

Самопроизвольные и несамопроизвольные процессы. Второй закон термодинамики, его формулировки и аналитическое выражение.

Энтропия. Статистическое толкование энтропии. Формула Больцмана. Расчет изменения энтропии в химических реакциях. Изменение энтропии как критерий направленности процессов в изолированных системах. Постулат Планка. Абсолютное значение энтропии. Термодинамические функции: функция Гельмгольца и функция Гиббса, использование их в качестве критерия направленности процессов в открытых системах. Способы расчета функции Гиббса для химических реакций. Энтальпийный и энтропийный факторы.

Химическое равновесие, его основные признаки. Константа химического равновесия, способы ее выражения и связь между ними. Закон действующих масс. Смещение химического равновесия. Принцип Ле Шателье. Уравнение изотермы химической реакции. Химическое сродство. Зависимость константы равновесия от температуры. Уравнение изобары и изохоры Вант-Гоффа. Смещение химического равновесия.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Термодинамика изучает законы, которые описывают обмен энергией между изучаемой системой и внешней средой и, в частности, переход тепловой энергии в другие формы энергий.

Химическая термодинамика – это раздел физической химии, изучающий превращения энергии в химических реакциях и энергетические характеристики различных веществ. Она основывается на положениях, законах и теоретических методах классической термодинамики. Применение химической термодинамики позволяет рассматривать процесс, не вдаваясь в механизм взаимодействия. Зная законы химической термодинамики, можно оценить, возможна ли реакция при данных условиях или невозможна, какие условия необходимо создать, чтобы реакция была возможной и чтобы выход продуктов был максимальным. Для решения этих вопросов термодинамическим методом необходимо знать только начальное и конечное состояние системы и внешние условия при которых она находится.

Таким образом, основными вопросами термодинамики являются энергетические балансы протекающих процессов и направления протекающих процесссов, включая состояние химического равновесия. Первая группа вопросов опирается на первый закон термодинамики, вторая – на второй и третий законы. Первый закон или первое начало термодинамики представляет собой постулат, вытекающий из многовекового опыта человечества. Он не имеет единой формулировки, поэтому существует несколько формулировок, которые равноценны между собой и вытекают одна из другой. Если одну из них рассматривать как исходную, то другие получаются из нее как следствия.

Первое начало термодинамики связано непосредственно с законом сохранения энергии и эквивалентности ее различных форм. Его формулируют в виде: в любой изолированной системе запас энергии остается постоянным.: различные формы энергии переходят друг в друга в строго эквивалентных количествах.

Одной из формулировок закона является такая: вечный двигатель первого рода невозможен, т.е. невозможно построить машину, которая бы давала механическую работу, не затрачивая на это соответствующего количества энергии.

Особенно важной для химической термодинамики формулировкой первого начала является выражение его через понятие внутренней энергии: внутренняя энергия является функцией состояния, т.е. ее изменение не зависит от пути процесса, а зависит только от начального и конечного состояния системы.

∆U = 0.

(1.1)

Изменение внутренней энергией ∆U системы может происходить за счет обмена теплотой Q и работой W с окружающей средой. Полученная системой извне теплота расходуется на приращение внутренней энергии и на работу, совершенную системой:

Q = ∆U + W.

(1.2)

Уравнение представляет собой математическую формулировку первого начала термодинамики для достаточно больших изменений данных величин (интегральная форма записи). Величины ∆U, Q и W в уравнении (1.2) могут иметь как положительные, так и отрицательные знаки. Например, если все три величины отрицательны, то теплота, отданная системой внешней среде, равна убыли внутренней энергии плюс полученная системой работа.

Для бесконечно малого изменения этих величин уравнение (1.2) примет вид (дифференциальная форма записи):

δQ = dU + δW.

(1.3)

В отличие от внутренней энергии теплота и работа не являются функциями состояния, они зависят от пути процесса, но разность их от пути процесса не зависит

	Q – W = ∆U	(1.4 а)
или	δQ – δW = dU.	(1.4 б)

Рассмотрим применение первого начала термодинамики к химическим процессам. Пусть в системе протекает химическая реакция по уравнению:

νАА + νВВ + … = νLL + νMM + …,

(1.5)

где νi – стехиометрические коэффициенты; А, В, L, M – символы реагирующих веществ и продуктов реакции соответственно.

Если считать, что единственным видом работы, которая совершается системой, является работа расширения т.е. отсутствует полезная работа, то уравнение (1.3) примет вид

	δW = рdV,	(1.6)
	δQ = dU + рdV.	(1.7)

Химические реакции протекают чаще всего в изобарных или изохорных условиях. При изохорном процессе (V = const, dV = 0) уравнение (1.7) примет вид

δQ = dU.

(1.8)

Интегральная форма записи данного уравнения будет следующей:

Q = U2 –U1 = ∆U.

(1.9)

Тепловой эффект реакции при постоянном объеме очень часто обозначают Q_v. Тогда

Qv = ∆U,

(1.10)

или в дифференциальной форме δQ_v = dU. (1.11)

Q = U2 –U1 = ∆U.

(1.11)

Таким образом, тепловой эффект химической реакции в изохорных условиях равен изменению внутренней энергии системы процесса.

При изобарных условиях проведения процесса (р = const), после интегрирования уравнения (1.7) и приведения подобных членов получим

Q = (U2 + рV2) – (U1+ рV1).

(1.12)

В химической термодинамике важное значение имеет термодинамическая функция – энтальпия, которая связана с внутренней энергией системы соотношением

H = U + рV.

(1.13)

Энтальпия, так же как и внутренняя энергия, является функцией состояния (так как pV – функция состояния). Из уравнений (1.12) и (1.13) получаем

Q = H2 –H1 = ∆H.

(1.14)

Тепловой эффект реакции при постоянном давлении обозначим Q_p.

Qp = ∆H,

(1.15)

или в дифференциальной форме

δQp = dH.

(1.16)

Таким образом, тепловой эффект химической реакции в изобарных условиях равен изменению энтальпии этого процесса.

Взаимосвязь изобарного и изохорного тепловых эффектов описывается уравнением:

∆H = ∆U + рΔV

(1.17)

Если реакция протекает в газовой фазе, то для состояния идеальных газов, с учетом уравнения PV = nRT, в изобарно–изотермических условиях рΔV == Δ nRT, уравнение (1.17) принимает вид

∆H = ∆U + ΔnRT

(1.18)

Из уравнений (1.10) и (1.15) следует, что для двух практически важных процессов: изобарного и изохорного – теплота процесса, являющаяся функцией процесса, приобретает свойства функции состояния, т.е. она не зависит от пути процесса, а зависит только от начального и конечного состояния системы. Это положение было сформулировано на основании опытных данных русским ученым Г.И. Гессом.

Формулировка закона Гесса. Тепловой эффект химической реакции при постоянном давлении или объеме не зависит от пути проведения процесса, а определяется только начальным и конечным состоянием реагентов и продуктов реакции при условии, что единственной работой, совершаемой системой, является работа расширения. Закон Гесса – математическое следствие первого начала термодинамики и составляет теоретическую основу термохимии.

ТЕРМОХИМИЯ

Раздел физической химии, занимающийся изучением тепловых эффектов химической реакции, называется термохимией. Термохимия позволяет экспериментально определять тепловые эффекты процессов, используя калориметрический метод исследования. Это могут быть не только химические реакции, но и физико-химические процессы, например, растворение, кристаллизация, сублимация и др. Кроме того, из закона Гесса вытекают важные следствия, которые позволяют теоретически рассчитать изменение энтальпии химических реакций.

Расчет тепловых эффектов химической реакции или изменения энтальпии реакции при заданной температуре (∆rH 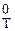) (индекс “r” обозначает “reaction”) можно провести используя справочные термодинамические данные стандартных энтальпий образования или энтальпий сгорания веществ.

Стандартной энтальпией (теплотой) образования вещества (∆fH ) (индекс “f “ обозначает “formation”) называется изменение энтальпии реакции образования одного моля вещества из простых веществ, взятых в устойчивом агрегатном состоянии, при стандартном давлении 101325 Па и отнесенные к температуре 298 К. Так стандартная энтальпия образования воды в жидком агрегатном состоянии равна изменению энтальпии реакции

H2(г) + ½O2(г) = Н2О (ж) ∆rH = –286,02 кДж/моль.

∆fH (Н2О(ж)) = ∆rH = –286,02 кДж/моль.

При этом энтальпия образования простых веществ (N2,O2,H2 и др.) принимается равной нулю.

Многие органические вещества нельзя синтезировать из простых веществ и одновременно определить стандартную энтальпию образования. Для органических соединений более легко определяемой экспериментально является энтальпия сгорания.

Стандартной энтальпией (теплотой) сгорания вещества (∆cH ) (индекс “с” обозначает “combustion”) называют энтальпию реакции полного окисления одного моля вещества c образованием высших оксидов.

Конечными продуктами сгорания для органических веществ соответствующего элементарного состава принято считать СО2(г), Н2О(ж), N2(г), С12(г), SO2(г) и т.д. Энтальпии сгорания СО2(г) и Н2О(ж) принимаются равными нулю. При этом необходимо иметь в виду, что теплоты образования СО2(г), Н2О(ж), SO2(г) тождественны теплотам сгорания простых веществ С(графит), Н2(газ), S (ромб)

С(графит) + О₂ (г) = СО2(г) ∆rH = –393,7 кДж/моль.

∆fH (С2О(г)) = ∆rH = –393,7 кДж/моль.

Используя сравнительно небольшое число справочных данных можно вычислить тепловые эффекты многих химических реакций.

Следствие 1. Стандартная энтальпия химической реакции равна разности стандартных энтальпий образования продуктов реакции и исходных веществ (с учетом стехиометрических коэффициентов):

∆rH = ∑νј ∆fH продуктов – ∑νі ∆fH исходных.

(1.19)

Следствие 2. Стандартная энтальпия химической реакции равна разности стандартных энтальпий сгорания исходных веществ и продуктов реакции (с учетом стехиометрических коэффициентов):

∆rH = ∑νi ∆сH исходных – ∑νj ∆сH продуктов.

(1.20)

Это следствие чаще используется для расчета тепловых эффектов реакций с участием органических соединений.

Термохимия вводит понятие “термохимическое уравнение”– это уравнение химической реакции, в котором, наряду с формулами исходных веществ и продуктов реакции, указаны стехиометрические коэффициенты, агрегатное состояние веществ и изменение энтальпии реакции, отнесенное к одному моль вещества. Например,

С(графит) + СО2(г) = 2СО(г) ∆_rH = –172,58 кДж/моль,

или С(графит) + СО2(г) = 2СО(г) + 172,58 кДж/моль.

Так как изменение энтальпии реакции относится к энергетическим изменениям в системе, то отрицательное значение ее (∆rH 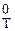< 0) соответствует экзотермическому процессу, а положительное (∆rH 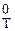> 0) – эндотермическому.

Преобладающее большинство термохимических данных в справочниках приведено при температуре 298 К. Однако, тепловой эффект химической реакции зависит от температуры. Данная зависимость в изобарных и изохорных условиях определяется уравнением Кирхгофа, дифференциальная форма которого имеет вид

	(d∆rH° / dТ)p = ∆rСр;	(1.21)
	(d∆rU°/ dТ)v = ∆rСv,	(1.22)

где, ∆rСр и ∆rСv – разность сумм молярных теплоемкостей (Ср, Сv) продуктов реакции и исходных веществ, взятых с учетом стехиометрических коэффициентов.

∆rСр = ∑νјСр 298 продуктов – ∑νіСр 298 исходных.

(1.23)

Дата добавления: 2015-10-31