Информационная энтропия. Энтропия в биологии

Информационная энтропия служит мерой неопределенности сообщений. Сообщения описываются множеством величин x₁, x₂ x_n, которые могут быть, например, словами: p₁, p₂ …, p_n. Информационную энтропию обозначают S_n или H_u. Для определенного дискретного статистического распределения вероятностей P_i используют следующее выражение:

при условии:

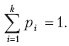
Значение S_n = 0, если какая‑либо вероятность P_i = 1, а остальные вероятности появления других величин равны нулю. В этом случае информация достоверна, то есть неопределенность в информации отсутствует. Информационная энтропия принимает наибольшее значение, когда P_i равны между собой и неопределенность в информации максимальна.

Общая энтропия нескольких сообщений равна сумме энтропий отдельных сообщений (свойство аддитивности).

Американский математик Клод Шеннон, один из создателей математической теории информации, использовал понятие энтропии для определения критической скорости передачи информации и при создании «помехоустойчивых кодов». Такой подход (использование из статистической термодинамики вероятностной функции энтропии) оказался плодотворными в других направлениях естествознания.

Понятие энтропии, как показал впервые Э. Шредингер (1944 г.), а затем Л. Бриллюэн и др., существенно и для понимания многих явлений жизни и даже деятельности человека.

Теперь ясно, что с помощью вероятностной функции энтропии можно анализировать все стадии перехода системы от состояния полного хаоса, которому соответствуют равные значения вероятностей и максимальное значение энтропии, к состоянию предельно возможной упорядоченности, которому соответствует единственно возможное состояние элементов системы.

Живой организм с точки зрения протекающих в нем физико‑химических процессов можно рассматривать как сложную открытую систему, находящуюся в неравновесном, нестационарном состоянии. Для живых организмов характерна сбалансированность процессов обмена, ведущих к уменьшению энтропии. Конечно, с помощью энтропии нельзя охарактеризовать жизнедеятельность в целом, так как жизнь не сводится к простой совокупности физико‑химических процессов. Ей свойственны другие сложные процессы саморегуляции.

[1]Формулировка принадлежит известному физику Д. Бому.

[2]ОТО – одна из самых сложных областей современной физики. Она базируется на громоздком математическом аппарате уравнений Эйнштейна, которые представляют собой систему ковариантных уравнений в частных производных.

Дата добавления: 2015-10-23