Математикалық әдісі

1. Терістеу .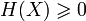

2. Шетеулері: , Йенсен теңсіздігінен вогнутты функция ушін 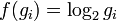және 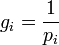. Егер 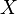-тің барлық n элементтері тең болса, .

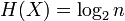3. Егер 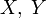тәуелсіз болса, онда .

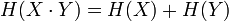4. Энтропия —мүмкін элементтерді орналастырудың томпақ жоғарғы функциясы.

Егер 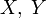бірдей элементтердің орналасуына ие болса, онда .

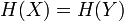Нәтижелілік

Алфавит біркелкіден алыс ықтималдықты үйлестіруге ие бола алады. Егер бастапқы алфавит 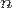символдан тұрса, онда оны мүмкін болған анықтауышы біркелкі «оптималданған алфавитпен» салыстыруға болады. Бастапқы және оптималданған алфавит энтропиясының арақатынасы — бұл процентпен берілетін бастапқы алфавиттің нәтижелілігі. 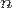символды бастапқы алфавиттің нәтижелілігі 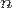-арлы энтропия арқылы анықталуыда мүмкін.

Энтропия шығынсыз теория жүзінде орындалуы мүмкін максималды қысуды шектейді (немесе мүлдем шығынсыз) – әдеттегі теру немесе, практикада, — Хаффмана, Лемпеля — Зива — Велча немесе арифметикалық кодтау.

Вариация және жалпылау

B энтропия

Жалпы жағдайда b энтропия (b тең 2, 3, …) қайнар көзі 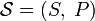бастапқы алфавитімен 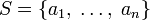және дискретті ықтималдықтарды үлестіру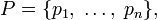 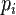ықтималдылығы 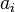(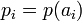), формуламен анықталады:

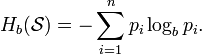
Мысалы:

Тринарлы энтропия

(b = 3) «чижды» (үшқырлы сүйектің түрі) лақтырғанда, тринарлы энтропия қайнар көзі («чиж») 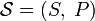бастапқы алфавитпен (сандар үшқырдың шегінде «чиж») 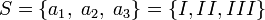және дискретті біркелкі ықтималдықтарды үйлестірумен («чиждың» қимасы —теңбағытты үшбұрыш, материал тығыздығы «чиж» барлық объектіге біртекті)

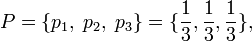
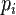ықтималдылығы 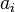(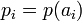) тең:

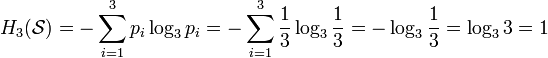
Тетрарлы энтропия

Төртқырлыны (b = 4) «чиж» лақтырғанда, тетрарлы энтропия қайнар көзі 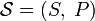бастапқы алфавитімен (сандар төртқырлының шегінде «чиж») 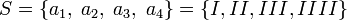және дискретті біркелкі ықтималдықтарды үйлестірумен (көлденең қима «чиж» — тіктөртбұрыш, материал тығыздығы «чиж» барлық объектіге біртекті «чиж»)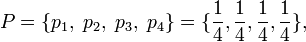 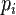ықтималдылығы 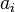(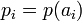), тең:

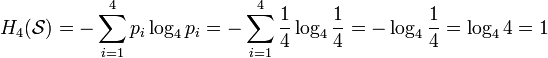тетрит.

Шартты энтропия

Егер алфавит символдарының ілесімі тәуелді болса (мысалы, француз тілінде «q» әріпінен соң әрдайым «u» әріпі ілеседі, ал «передовик» сөзінен соң газеттерде «производства» немесе «труда» сөздері ілеседі), мұндай символдар бірізділігінен тұратын ақпарат саны.Бірінші шарттың энтропиясы (біріншісі Марков үлгісі үшін бір әріп пайда болу ықтималдығы белгілі) деп аталып жатыр (екі әріпті тіркестердің) ықтималдықтары:

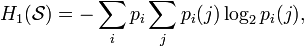
Бұл алдыңғы нышаннан тәуелді болатын және бұл ықтималдық шартта, не алдыңғы нышанмен еді.

Мысалы, «е» [3] әріпсіз тіл орысы үшін.

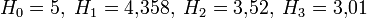
Дербес және ортақ шартты энтропиялар арқылы осы бөгеттермен каналда берілуде ақпараттық жоғалтулар толық суреттеліп жатыр. Матрица қолданылып жатыр. Тараптармен көз жоғалтулар сипаттама үшін (біресе жіберған сигнал) белгілі бар шартта нышанның қабылдағышпен алудың шартты ықтималдығы қарап жатыр. Бұл каналда матрица келесі түрде болады:

			…		…
			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…

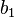
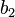
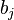
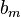
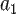
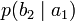
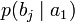
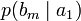
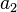
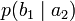
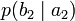
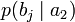
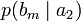
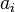
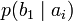
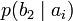
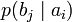
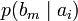
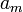
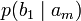
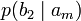
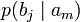
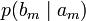
Анық, диагональ бойынша орналасқан ықтималдыққа, дұрыс қабылдаудың ықтималдық суреттеп жатыр, ал бағанасының барлығын элементтерінiң сома — қабылдағышқа лайықты нышанның пайда болулар ықтималдығын беріп жатыр. Берілетін сигналға келетін жоғалтуды, дербес шартты энтропия арқылы суреттеледі

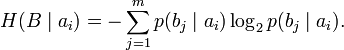
Барлығын сигналдарында берілуде жоғалтулар есептеу үшін ортақ шартты энтропия қолданылады:

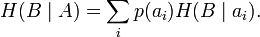
Тараптармен көздің энтропияны білдіріп, тараптармен қабылдағыштың энтропияға ұқсас қаралып, орнына барлық жерде көрсетіліп жатқан жолдар элементтері ықтималдық болып тұр

Өзара энтропия

Өзара энтропия немесе біріктірулер энтропиясы статистикалық тәуелді қатынастар.Энтропия өзара байланысты жүйелер энтропия есеп айырысу үшін арналған және белгі қойған хабарлағышты мінездейді.

Тапсырған және алған сигналдардың өзара байланыс бірлескен оқиғалардың ықтималдықтармен суреттеліп, және канал мінездемелер толық сипаттама үшін тек қана бір матрица керек болады:

		…		…
		…		…
…	…	…	…	…	…
		…		…
…	…	…	…	…	…
		…		…

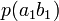
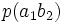
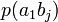
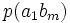
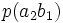
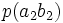
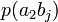
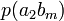
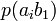
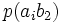
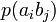
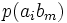
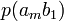
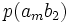
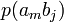
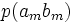
Канал емес суреттелген кезде, ортағырақ жағдай үшін, ал жүйелер, матрица бүтін өзара жұмыс істеп, квадрат болмауы тиісті емес. Анық, нөмірімен бағанасының барлығын элементтерінiң сома беріп жатыр, нөмірмен жолдар сомасы бар, ал матрицалары барлығын элементтерінiң сомасы 1 тең. Оқиғалардың бірлескен ықтималдығы және бастапқы және шартты ықтималдықтар шығарманы сияқты есептеп жатыр:

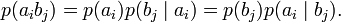
Байес формуласы бойынша шарт мүмкіндігі орындалады. Осылайша, кабылдау және энтропия қорын есептеуге бүкіл мәліметтер бар.

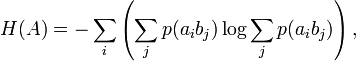
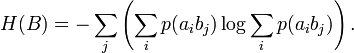
Өзара энтропия олардың логарифм көбейтіндісі, бүкіл мүмкін матрицаларды жол бойынша (баған) реттелген қосу арқылы есептеледі.

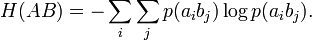
Өлшеу бірлігі- бит/екі символы,бұл былайша түсіндіріледі: өзара энтропия жұпты символ анықталмағанын суреттейді.Олар: анықталған және алынған болып бөлінеді.

Қарапайым түрлендіру арқылы аламыз:

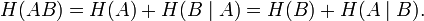
Өзара энтропия ақпаратты толық мәніне ие – осыдан қарастырылып отырған көлемдерді алуға болады.

Тарихы

1948 жылы, ақпараттың тиімді берілісінің мәселесі арқылы шумдалған коммуникациялық арнаны зерттей келе, Клод Шеннон коммуникацияның түсінушілікке революционерлік мүмкіндіктің тіл табуын ұсынды және энтропиянің бірінші шынайы математикалық қағидасын жасады. Оның сенсациялық идеялары екі негізгі бағыттың құрылуына негіз болды, олар: ақпарат теориясы, эгродиялық теорияның және мүмкіндік түсінігін коммуникациялық жүйе және статиқалық мінездеме мәліметтерін қолданады, және кодтау теориясы негізі алгебралық және геометриялық құрылғыны эффективті кодты ұйымдастыру үшін қолданады.

Шеннон мақаласында «A Mathematical Theory of Communication» энтропия түсінігі берілген, 1948 жылы екі мақалада жарияланған Bell System Technical Journal.

Бақылау сұрақтары:

1. Ақпараттық энтропия дегеніміз?

2. Бүгінгі күнде энтропияның қандай түрлері белгілі?

3. Шеннон бойынша анықтау

4. Анықтау өздік ақпарат бойынша

5. Математикалық құрам

6. Энтропияның тиімділігі

Тақырып 3. Ақпарат саны және артықшылық. Ақпаратты тасымалдау жылдамдығы.

Лекция мақсаты: Артықшылық түсінігін зерттеу

Сұрақтар:

1. Ақпарат көлемі және энтропия өзара қалай байланысқан?

2. Артықшылық түсінігін анықтау

3. Хабарламадағы ақпарат көлемін анықтау, к тең емес мүмкіншілікпен құрылған

4. Дифференциалды энтропияға анықтама беріңіз және оның негізгі сипатын құрастырыңыз

Егер бүкіл анықталмағандық алынса, ақпарат энтропияға тең

І = Н,

Қарсы жағдайда- бастапқы және соңғы энтропия арасындағы айырмашылық

I =H₁-H₂ (3.1)

Егер барлық оқиғаның мүмкіндіктері бірдей болса, ақпараттың көп саны алынады, егер толықтай ең көп белгісіздік түсіндіріледі -.

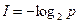=Н_макс

Ақпараттың артықшылығы - ытималдың арасында ақпарат көлемі және энтропиямен болуы:

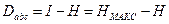(3.2)

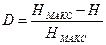
Ақпараттың саны сияқты хабарламаның ортақ санының мумкін ұсынысы туындысын к ортаның энтропияснда:

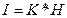
Алғашқы әліпбинің тең мүмкінді және өзара тәуелсіз символ оқиғасы үшін ақпараттың саны арада к m әліпбиінің хабарламаларында тең:

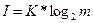(бит).

Символдық алфавиттегі тең емес ықтималдық этнропиясы:

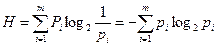(бит/символ),

Ықтималдық символы - Ақпараттың хабарлама саны

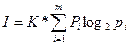
Ақпараттар саны келесідей талаптарды қанағаттандырады:

1. Ақпараттар саны екі тәуелсіз хабарламалардың тен қосындылары, яғни әрбір ақпараттың санында.

2. Жағдайды таңдау мүмкіншілігінің жоғарылауы монотонды қажеттілігі.

3. Шынайы оқиғаларға толы ақпараттар санының құрамында белгісіздік нолге тең

4. Ақпарат санының тәуелсіздігі хабарламарың сапасынан, әсіресе хабарлама алушының маңыздылық дәрежесінен, салдарының мүмкіншілік дәрежесінен және т.б.

Дата добавления: 2015-10-23