
|
Читайте также: |
Дәрістің мақсаты: Хемминг кодын үйрену. Кедергіге төзімді кодалау түсінігі
Сұрақтар:
1. Кедергіге қалыпты қарсы тұратын кодтар дегеніміз не?
2. Хэмминг коды?
3. Хэмминг коды не үшін қолданылады?
4. Қателерді өңдеу несімен көмектеседі?
Кедергіге төзімді кодалау
Кодалы аймақ
Шулы дискретті арнаның басты теоремасы бойынша, ақпарат жасаудың жылдамдығы арнаның өткізу қабілетіне тең немесе одан кем болса, онда ақпараттың арна бойынша аз қателікпен жіберуге мүмкіндік беретін коды болады. Бірақ ол хабарлауды максималды жылдамдықпен және минималды қателікпен кодалау мәселесін шешпейді, яғни кедергіге төзімді кодалау мәселесін шешпейді. Бұл мәселені шешудің арнайы әдістері бар. Кең қолданысқа ие: алгебралық әдіс, оның көмегімен группалық кодтар класы зерттелді, және геометриялық кодтар.
Кодтық аяның құрылысын біркелкі кодаға қолданып қараймыз, дербес жағдайда блоктық, кодалық комбинациялар бір біріне тәуелсіз кодталады және декодталады. Шығу алфавиті В біркелкі n-ретті коды,Г m символдан құралады; mсаны коданын негізі деп аталады. Осындай кодтың кодалық комбинациясының түрі мынадай 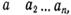 мұнда
мұнда  мағынасы
мағынасы  ші разрядты коды,
ші разрядты коды, 
 алфавит символын реттейміз және m модулі бойынша есептеудің әртүрлі символды классы екенін түсінеміз. Индекс классын m санын қалдық өкіліне бөлгенде қоямыз.
алфавит символын реттейміз және m модулі бойынша есептеудің әртүрлі символды классы екенін түсінеміз. Индекс классын m санын қалдық өкіліне бөлгенде қоямыз.
Көптік В-ге екі алгебралық операцияны енгізейк: көбейту мен қосуды-  , Cr классы мұнда,r-бөлген кездегі қалдық m –ді
, Cr классы мұнда,r-бөлген кездегі қалдық m –ді  және классты сумма
және классты сумма 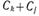 класс
класс  егер
егер  және
және  егер
егер  .
.
2.5-те көрсетілгендейкөп класстар m модулі бойынша енгізілген қосу және көбейту амалдары көрсетілген аймақ болады. Бұл кодалық комбинацияға мұрша береді В шығу алфавитіндегі n-ретті
бірретті коданы аймақ үстіндегі сызықты n векторы ретінде қарастырады. Бұл аймақты ары қарай кодалық аймақ деп,ал оның элементтерін кодалық вектор деп қарастырамыз. m модулді операцияларды жеңілдету үшін оларды ары қарай 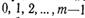 белгілейміз.
белгілейміз.
Қодалық аймақта кодалық векторлар қателігін дұрыстау анализі нәтижесінде метрика енгізеді. Қолданысқа ие Ли мен Хэмминг метрикасы.
Метрика Ли анықтамасын анықтау үшін вектор весі ұғымын қолданамыз
Мұнда 

Ли арақашықтығы  вектор арасында
вектор арасында 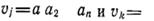
 , бұл
, бұл  вектор салмағының артүрлігі деп аталады.
вектор салмағының артүрлігі деп аталады.
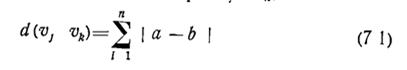
Кең қолданысқа ие блотық кодаларды құру кезінде Хэмминг метрикасын қолданады.
Қателерді өңдеу
кедергіге қалыпты қарсы тұратын кодтар тек қана қателерды анықтауды ғана жүзеге асырмай сонымен қатар оларды өңдейді. Qm нан аспайтын еселіктердың қателеіктерін өңдеудің жалпы идеясы келесіде. М кедергіге қалыпты қарсы тұратын қодтардың мүмкін болатын кодалық комбинациялары N класына бөлінеді. Бұл бөліну әр классқа бір рұқсат етілген және оған жақын рұқсат етілмеген кодалық комбинация кіру керек. Қайта кодалау кезінде қабылданған кодалық комбинация кай классқа жататынын анықталады. Егер де кодалық комбинаия қатеиен қабылданса, яғни рұқсат етілмеген, онда ол ол классқа жататын рұқсат етілгенге өңделеді. Кодалау теориясында Qm нан аспайтын еселіктердың қателеіктерін қңдеу мүмкіндіктерін жүзеге асыру үшін кодалық ара-қашықтық 2qm нан көп болу керек екені дәлелденген. Көбіне ол  формуласымен анықталады. n разрядты екілік кодты N кодалық комбинациясының ең үлкен санын d қашықтықпен табу ерекше болып саналады.
формуласымен анықталады. n разрядты екілік кодты N кодалық комбинациясының ең үлкен санын d қашықтықпен табу ерекше болып саналады.
Кодалау теориясында келесі өрнектер бар:
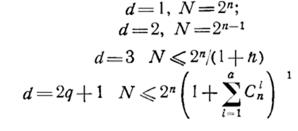
Хэмминг коды
(n,k)-кодының мысалы ретінде ара – қащықтығы 3ке тең және дара қателіктерді өңдейтін Хэмминг кодын алайық. Кодалық ара-қашықтығы d=3 ке тең коды үшін рұқсат етілген сан 7,5 – тақырыпта көрсетілгендей 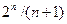 ге тең. Хэмминг коды үшін бұл теңсіздік теңдікке айналады. Кодтың кодалық комбинациясының алғашқы к разряды ақпараттық ретінде қолданылады, және ол келсіге тең
ге тең. Хэмминг коды үшін бұл теңсіздік теңдікке айналады. Кодтың кодалық комбинациясының алғашқы к разряды ақпараттық ретінде қолданылады, және ол келсіге тең
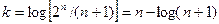
Бұл теңдеу Хэмминг кодын анықтайтын бүтін санды мәнді к=0,1 4,11 26,..., береді: (3,1)-код, (7,4)-код, (15,11) – код және т.б.
Бақылау сұрақтары:
5. Кедергіге қалыпты қарсы тұратын кодтар дегеніміз не?
6. Хэмминг коды?
7. Хэмминг коды не үшін қолданылады?
8. Қателерді өңдеу несімен көмектеседі?
Дата добавления: 2015-10-23; просмотров: 764 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тақырып 11. Кодтардың префикстілігінің тиімділік талаптары. Қарапайым (бөгеуілорнықтылықсыз) кодтар. | | | Тақырып 13. Кедергіге төзімді кодалау. Кодалы арақашықтықпен түзетуші қабілеті бар кодалардың байланысы |