Тақырып 9. Үздіксіз хабарлама көзі мен үздіксіз байланыс арналарының ақпараттық сипаттамалары.

Дәріс мақсаты:

1. Үздіксіз хабарлама көзінің ақпараттық сипаттамаларын зерттеп тану.

2. Үздіксіз байланыс арналарының ақпараттық сипаттамалары

Сұрақтар:

1. Эпсилон түсінігі.

2. Үздіксіз хабарлама көзі мен ақпараттық сипаттамалары қандай?

3. Үздіксіз байланыс арналарының ақпараттық сипаттамалары қандай болады?

1. Үздіксіз хабарлама көзі ақпараттық сипаттамалары

Эпсилон- үздіксіз хабарлама көзінің өнімділігі. Нақты түрде Үздіксіз хабарлама (t) кез келген процестің Т уақыт аралығында қандай да бір орындауын білдіреді. Үздіксіз хабарлама көзін орындау ансамблімен сипатталады. Ең өнімді модель ол эргодикалық кездейсоқ процесс түріндегі үздіксіз хабарлама болды.

Үздіксіз хабарлама көзінің өнімділігін анықтау үшін ε –кездейсоқ шаманың энтропиясы анықталған § 3.7 қорытындысы мен жолын қолданады.

Берілген ε ықтималдылықпен кез келген (t) орындау үшін бірлік уақытта құрылатын, минималды ақпарат санымен үздіксіз хабарлама көзі Ηε(z) ε-өнімділігімен түсіндіріледі.

(t) uT(t)-ның жүзеге асырылуы арқылы қайталанады деп есептейік. Бақыланып отыратын жүзеге асыруларды шектеулі немесе жеткілікті жалпақ спектрлі F [28, 8] сигнал деп қарастыруға болады. Жеткілікті мөлшердегі үлкен ұзақтықта Т (t) немесе uT(t) ретінде де N-шамалы (N = 2FT) векторы ретінде және санау болып табылатын (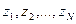) және () координаттары түрінде де көрсетілуі мүмкін. { (t)} хабарламасының ансамблі және {uT(t)} қайталанушы сигналдарды Ζ1, Z2,.., ZN и U1, U2,.., UN кездейсоқ шамаларына сәйкес келетін N-шамалық кездейсоқ Ζ және U векторларын сипаттайды. Ансамбльдің әрқайсысының статистикалық сипаттамасы N-шамалық ықтималдықты тарату тығыздығымен ρ(Ζ) = ρ(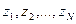) және p(U) = p() беріледі. Ансамбльдер арасындағы байланыс pu(Z)= ρ(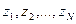 / ) және pz(U) = p( / 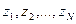) ықтималдықты тарату шартты тығыздығы және ықтималдықты таратудың сәйкес тығыздығымен p(Z,U) = p(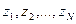; ) көрсетіледі.

(4.20) формуласын кеңейту арқылы N-шамалық Ζ және U кездейсоқ векторлары ақпараттық саны үшін олардың біріншісі екіншісіне салыстырмалы түрде келесі формуланы аламыз:

Мұнда интеграл N-шамалы болып саналады.

Туралықтың орташашаршылық критерийін (Z,U), қолданамыз, және оны келесідей түрде қарастырамыз:

Мұнда, p(Z,U)ZU ара қашықтық шаршысын l(Z,U) N-шамалы евклидтық кеңістікте көрсетіледі.

Бір дискреттік сигналдарды ZT(t) және UT(t) есептеуге өтуші ақпараттардың саны келесідей жолмен анықталады:

ε-пропорционал үздіксіз хабарламалар көздері Нε(Z) сай анықтама үшін келесідей жазамыз:

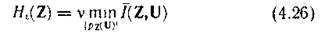
Шартты орындаған жағдайда:

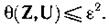
ν шамасы есептеу көздерінің құрылу жылдамдығын сипаттайды (ν = =2F).

Мысал 4.5. ε-өнімділік көзін ν₁ жылдамдығымен жасалған өзара байланыссыз σ2дисперсиясымен тұрақты орташа кездейсоқ сигналдардың есептеулерін анықтау.

(3.65) алынған орташа таратылған кездейсоқ шамасын ε-энтропиясын қолдана отырып, табамыз:

Кез келген zT(t) хабарламасын берілген туралықпен қайта есептеу мүмкіндігі геометриялық түсінікті береді. Эргодикалық процестердің жүзеге асырылуы жеткілікті ұзақ уақытта типтік болып табылады және бірдей орташа қуаттылыққа ие болады, N-шамалық кеңістіктегі векторларға үзіліссіз көп нүктелерден тұратын хабарламалар тең өшірілген координаттар басынан (гиперсфера) құралған.

Қайталанатын сигналдардың соңғы көпшілігі UT(t) қиылыспайтын түзу сфералық N-бұрыштардың орталығында (ε-аймағы) гиперсфера аралықсыз дамиды. ε-аймағының өлшемі хабарламаны берілген қайталау туралығы үшін анықталған. Егер түпнұсқасы болып z*T(t) хабарламасы жүзеге асырылып, ε-аймағы түсуі керек вектордың соңы u*T(t) сигналына түссе, онда u*T(t) сигналы қайталанады.

Көрсете кететін жайт, қайталанудың берілген туралығы, тек хабарламаның жеткілікті үлкен ұзақтығында ғана, бірлікке жақын ықтималдықпен жетеді, үзіліссіз жүзеге асырылулардың жүйелілігінде есептеулерді елемеуге де болады. Берілген қате жіберулерді Т хабарламаның шектеулі ұзақтығында азайтуда N есептеулерінің санын ұлғайту керек. N→∞ шегінде үзіліссіз жүзеге асырылуларды алуға болады.

ε – өнімділік көзін есептен шығаруда және хабарламларды қайталау мүмкіндігін берілген туралықпен геометриялық түсіндіруде, негізінде, еш нәрсе өзгермейді. Тек қана, N-шамалы евклидово хабарламалар кеңістігі гильберттік болады және екі сигналдың жақындық шамасы осы кеңістік ара қашықтығындай болуы керек.

Дата добавления: 2015-10-23