Сигнал сипатының уақытша формасы

Сигналдың уақытша сипаттамасы дегеніміз U(t) сигналының таралуын айтамыз. Мұнда базисті функция ретінде бірлік ипульсті функция – дельта-функция қолданылады:

Дельта-функцияның символды орналасуы келесі суретте көрсетілген:

d(t- x₁)­:

½:

½½

½½

½½ t

0 x

5-сурет

Нақты сигналды сипаттайтын жалғыз ғана параметр болып оның қозғалыс уақыты болып табылады. d функциясы көмегімен нақты сигналды жазуға болады:

(5.5)

u(t) функциясы бір-біріне жалғасып жатқан шексіз аз ұзақтылықты импульс түрінде сипатталған. (5.5)- формула сызықты жүйелер теориясында ерекше орын алады.

Негізгі әдебиет: 2[18-24]; 6[43-47];

Қосымша әдебиет: 13(20-23]; 161147-157].

Бақылау сұрақтары:

1. Детерминдендірілген сигнал дегеніміз не?

2. Детерминдендірілген сигналдардың математикалық ұсынылу түрлері.

3. Функция жүйесінің ортонормаланғандық және ортогональдік шарттарын жазыңыз.

4. Детеминдендірілген сигнал модельдерін білу не үшін қажет?

5. Сигналдарды көрсетудің уақыттық қалыбын сипаттаңыз.

Тақырып 5. Кездейсоқ процесс- сигналдың моделі ретінде. Кездейсоқ процестердің ықтималдылық сипаттамалары. Стационарлы және эргодикалық кездейсоқ процестер.

Лекция мақсаты: Кездейсоқ сигналдармен танысу.Іске асыру ансамбліне анықтама беру. Кездейсоқ процестер моделдеу. Кездейсоқ шамаларды бірқалыпты тарату.

Сұрақтар:

1. Кездейсоқ сигналдар түсінігі және оларды іске асыру ансамблі.

2. Кездейсоқ модельдер ансамбльдері қалай құрылады?

3. Кездейсоқ шамаларды бірқалыпты тарату.

4. Кездейсоқ процестің ықтималдық сипаттамалары қандай?

Біз қалыбын дәл білетін детерминдендірілген сигналдарға қарағанда, кездейсоқ сигналдардың лездік мәндері алдын-ала белгісіз, тек қандай да бірден аз ықтималдықпен болжануы мүмкін. Мұндай сигналдар сипаттамалары статикалық, яғни ықтималды болып табылады.

Радиотехникада ықтималдық сипаттаманы қажет ететін екі негізгі сигналдар класы бар. Біріншісі, бұл шулар – әртүрлі физикалық жүйелерде заряд тасымалдаушыларының ретсіз қозғалысы себебінен туындайтын, уақыт бойынша хаостық өзгеретін электромагниттік тербелістер. Екіншісі, кездейсоқ сигналдар дегеніміз ақпарат таситын барлық сигналдар болып табылады, сондықтан байыпты хаттамаларға тән заңдылықтарды сипаттау үшін де ықтимал модельдерге жүгінеді.

Іске асыру ансамблі

Уақыт бойынша өзгеретін кездейсоқ сигналдық математикалық моделі кездейсоқ процесс деп аталады. Анықтама бойынша Х(t) кездейсоқ процесі – бұл ол кез-келген t уақыт мезетінде қабылдайтын мәндер кездейсоқ шама болып табылуымен сипатталатын кездейсоқ түрдегі функция.

Тіркеуге дейін (қабылдауға дейін) кездейсоқ сигналды ортақ статикалық заңдылықтарға жүгінетін, x_i(t) уақыт функцияларының жиынтығы (ансамблі) ретінде көрініс беретін кездейсоқ процесс ретінде қарастырған жөн. Хаттаманы қабылдаған соң толықтай белгілі болған осы функциялардың бірі кездейсоқ процестің іске асырылуы деп аталады.Бұл іске асыру енді кездейсоқ емес, детерминдендірілген уақыт функциясы. 1 –суретте бірнеше кездейсоқ процесті іске асырудың мысалы келтірілген.

3. Кездейсоқ процесстер салыстырмалы жиілігі нұсқалған сипаты ретінде көрініс бере алады. Осылайша берілетін кездейсоқ процестер моделдеріне бірнеше мысал келтірейік.

x₁(t)

t₁ t₂ t

x₂(t)

t₁ t₂ t

x₃(t)

t₁ t₂ t

1 сурет- Кездейсоқ процесстердің жүзеге асуы

Кездейсоқ бастапқы фазалы гармоникалық сигнал

Көптеген практикалық мәселелерде кездейсоқ процесс моделі қолданылады, олардың орындалу амплитудасы және жиілігі белгілі (детерминдендірілген) болатын гармоникалық тербелісті көрсетеді. Қарастырылып отырған кездейсоқ процестің орындалуын былай жазуға болады:

Мұнда, А – амплитуда (детерминдендірілген), ω₀ – жиілік (детерминдендірілген) және φ – кездейсоқ бастапқы фаза, ол көптеген қызықты практикалық жағдайларда 0…2π интервалында біркелкі бөлінген деп саналады, яғни келесі ықтималдық тығыздығына ие:

,басқа жағдайларда

x(t)

0 t

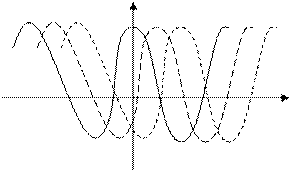
2 сурет - Кездейсоқ бастапқы фазалы гармоникалық сигналдың орындалуы.

Берілген кездейсоқ процестердің орындалуының бірнеше графиктері, бір-біріне қатысты уақыт осі бойынша жылжыған синусоидалар 2 суретте көрсетілген.

Көріп тұрғандарыңыздай, осы жағдайдағы процесстің орындалуының нақты түрі жай ғана кездейсоқ өлшемнің мәнімен – бастапқы фазамен анықталады.

Кездейсоқ телеграфты сигнал. Орындалуы +1 және -1 мәндерін қабылдайтын кездейсоқ процесс, әрі деңгей айырмасы уақыттың кездейсоқ сәттерінде болады және τ уақытта өтетін деңгей айырымының саны N, Пуассон заңымен суреттелетін ықтималдықтың дискретті бөлінуі бар кездейсоқ өлшем болып табылады:

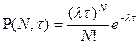(1)

Мұнда, λ – деңгей айырымының туындауының орташа жиілігін анықтайтын оң параметр.

Деңгей секірісі t_k уақыттың кездейсоқ сәттерінде болады, сондықтан берілген кездейсоқ процесстің жеке орындалуы үшін аналитикалық түрде формуласын жазу анағұрлым қиын екен, ал оның графигін тек шартты түрде ғана салуға болады.

x(t)

t

-1

3 сурет – Кездейсоқ телеграфты сигналдың графигі.

Бұл жағдайда нақты орындалу алуан шексіз кездейсоқ өлшемдер – t_k деңгей айырымының моменті арқылы беріледі, ал кездейсоқ процестің сипаттамалары осы кездейсоқ өлшемдердің статистикалық қасиеттерімен анықталады.

Сонымен, кездейсоқ процестің толық сипаттамасы оның орындалу ансамблін береді. Алайда практикалық есептерді шешу үшін сандық параметрлер және детерминдендірілген функциялар түрінде көрсететін анағұрлым қарапайым сипаттамалар жеткілікті. Ол жөнінде кейін айтылады.

Бұл жағдайда нақты орындау көптеген шексіз кездейсоқ өлшемдермен беріледі, момент деңгейінің айырмасы t_k, ал кездейсоқ процесстің сипаттамасы осы кездейсоқ өлшемдердің статистикалық қасиеттерімен анықталады.

Сонымен, кездейсоқ процестің толық сипаттамасы оның орындау ансамбліне береді. Бірақ практикалық есептерді шешу үшін көп жағдайда сандық параметрлерімен және детерминдендірілген функциялар түрінде берілген жай сипаттамалар жеткілікті. Келесі кезекте, бұл туралы айтылады.

Дата добавления: 2015-10-23