Пример решения задач. Задача 1. Находящийся при нормальных физических условиях воздух объемом 10 м3 сжимается

Задача 1. Находящийся при нормальных физических условиях воздух объемом 10 м³ сжимается обратимо до конечной температуры 400ºC. Сжатие производится изохорно, адиабатно, изобарно, политропно с показателем n =2,2. Считать воздух идеальным двухатомным газом с m=28,97 кг/кмоль; использовать теоретические значения теплоемкостей. Определить энтропию воздуха в конце каждого процесса, принимая ее равной нулю в исходном состоянии.

Решение

а). Находим массу воздуха:

.

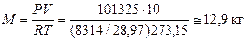б). Находим с_v, с_p, k= с_p/ с_v, с _п = с_v (n–k)/(n –1):

; ; ;

c_p =1004,5 Дж/(кг К)@1,005 кДж/(кг К).

k= с_p/ с_v =7/5=1,4. c _п=717,5(2,2–1,4)/(2,2–1)=521,8 Дж/(кг К).

в). Определяем изменение энтропии в каждом процессе.

1. Изохорный процесс. Из формулы (6.2) следует (т.к. s ₁=0)

;

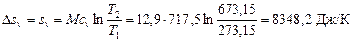2. Изобарный процесс. Из формулы (6.3) следует

.

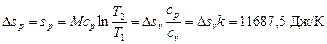3. Адиабатный процесс. Поскольку процесс обратимый, то это одновременно и изоэнтропийный процесс:

4. Политропный процесс (dS = Mc _п dT/T)

.

Задача 2. В сосуде объемом V =300 л заключен воздух при давлении P ₁=5 МПа и температуре t ₁=20ºC. Параметры среды: P ₀=0,1 МПа, t ₀=20ºC. Определить максимальную полезную работу, которую может произвести сжатый воздух, считая его идеальным двухатомным газом.

Решение

а). Переводим величины в единицы СИ: V =300·10^–3 м³ = 0,3 м³; P ₁=5·10⁶ Па; T ₁=293,15К.

б). В конечном состоянии P ₂= P ₀, T ₂= T ₀= T ₁. Так как газ идеален, а T ₂= T ₁, то du =0 и D u =0 (закон Джоуля).

В соответствии с (6.5), т.к. D u =0, для 1 кг воздуха

ex = T ₀(s ₂– s ₁)– P ₀(v₂ – v ₁) (Дж/кг).

Из (6.3) получаем

D s = s ₂– s ₁ = R ln(P ₁ /P ₂) = (8314/28,97)·ln(5/0,1)@1,123 кДж/(кг·К).

Масса воздуха

М = P ₁ V ₁/ RT ₁ @ (5·10⁶·0,3)/(287·293)=17,84 кг.

v ₁= V / M =0,0168 м³/кг; v ₂= v ₁ P ₁/ P ₂ = 0,841 м³/кг; V ₂= v ₂ M =15 м³;

ex @293·1123–10⁵(0,841–0,0168)=245,5 кДж/кг.

Для всей массы воздуха получаем

Ex= M ex @ 4377 кДж.

Задача 3. В проточном теплообменнике нагревается воздух. Параметры воздуха на входе в теплообменник: P ₁=0,7 МПа, t ₁=140ºC, на выходе P ₂=0,63 МПа, t ₂=800ºC. Параметры среды: P ₀=0,1 МПа, t ₀=15ºC. Определить изменение эксергии 1 кг потока воздуха в теплообменнике. Воздух считать идеальным газом.

Решение

а). Переводим величины в единицы СИ: P ₁=7·10⁵ Па; T ₁=413,15К; P ₂=6,3·10⁵ Па; T ₂=1073,15 К; P ₀=10⁵ Па; T ₀=288,15К.

б). Из уравнения (6.6) для эксергии потока на входе и выходе получаем (для 1 кг воздуха)

ex ₁= h ₁– h ₀– T ₀(s ₁– s ₀),

ex ₂= h ₂– h ₀– T ₀(s ₂– s ₀).

Изменение эксергии

d = ex ₂– ex ₁ = h ₂ – h ₁ – T ₀(s ₂– s ₁),

D h = h ₂ – h ₁= c _p (T ₂ – T ₁) (закон Джоуля),

D s = s ₂ – s ₁ = с_p ln(T ₂ /T ₁) – R ln(P ₂ /P ₁) (уравнение (6.3)),

D h= 1004,5(800–140)@663 кДж/кг,

D s= 1004,5·ln (1073,15/413,15)–(8314/28,97)·ln(63/70)@989 Дж/кг.

T ₀D s= 288,15·989@285 кДж/кг.

Окончательно

d= 663–285 = 378 кДж/кг.

Задачи

6.1. 1 кг воздуха сжимается обратимо от P ₁=1 бар и t ₁=15ºC до P ₂=5 бар и t ₂=100ºC. Определить изменение энтропии. Теплоемкость считать постоянной.

6.2. Определить изменение энтропии в процессе испарения 3 кг азота в политропном процессе при изменении температуры от t ₁=100ºC до t ₂=300ºC. Показатель политропы n =1,2. Теплоемкости принять по молекулярно-кинетической теории. Изобразить процесс в P-v- и T-s- диаграммах.

6.3. Определить изменение энтропии в процессе испарения 1 кг воды при температуре, равной 100ºC, если известно, что теплота парообразования r =2257 кДж/кг.

6.4. 50 кг льда с начальной температурой –5ºC помещены в воздух с температурой +15ºC. Считая, что образующаяся при таянии вода нагреется до температуры воздуха, определить увеличение энтропии, происходящее в результате этого процесса. Теплота таяния льда l=333 кДж/кг, теплоемкость льда с_p = =2,03 кДж/(кг·К). Теплоемкость воды принять равной 4,187 кДж/(кг·К).

6.5. Определить приращение энтропии 3 кг воздуха а) при нагревании его по изобаре от 0 до 400ºC; б) при нагревании его по изохоре от 0 до 880ºC; в) при изотермическом расширении с увеличением объема в 16 раз. Теплоемкость считать постоянной.

6.6. Средняя теплоемкость алюминия с_p в интервале температур от 0 до 300ºC равна 0,955 кДж/(кг·К). Определить энтропию 100 кг алюминия при 300ºC, считая, что его энтропия при 0ºC равна нулю.

6.7. 1 кг воздуха сжимается по политропе от 1 бар и 20ºC до 8 бар при n =1,2. Определить конечную температуру, изменение энтропии, количество отведенного тепла и затраченную работу.

6.8. В процессе политропного расширения воздуха температура его уменьшилась от t ₁=25ºC до t ₂= –37ºC. Начальное давление воздуха P ₁=4 бар, количество его m =2 кг. Определить изменение энтропии в этом процессе и конечное давление воздуха, если известно, что количество подведенного к воздуху тепла составляет 89,2 кДж.

6.9. 30 л воды с температурой 90ºC смешиваются с 20 л воды с температурой 15ºC. Определить вызванное этим процессом изменение энтропии. Теплоемкость воды принять равной 4,187 кДж/(кг·К). Считать, что тепловые потери отсутствуют.

6.10. Стальной шар массой 10 кг при 500ºC погружается в сосуд с 18 кг воды, температура которой равна 15ºC. Определить изменение энтропии системы в этом процессе. Считать, что тепловые потери отсутствуют. Теплоемкость принять равной 0,5129 кДж/(кг·К), теплоемкость воды 4,187 кДж/(кг·К).

6.11. Определить энтропию 1 кг газовой смеси, состоящей из азота и аргона, при P ₁=0,3 МПа и t₁ =300ºC. Массовые доли азота и аргона: g _N2=0,37, g _Ar=0,63. Газы считать идеальными; принять, что при P ₀=0,1 МПа и t ₀=0ºC энтропии азота и аргона равны нулю.

6.12. Определить, насколько увеличится энтропия при смешении 3 кг азота и 2 кг углекислого газа. Газы считать идеальными. Температура и давление газов до смешения одинаковы.

6.13. Определить эксергию воздуха в баллоне. Давление воздуха в баллоне 15 МПА, температура равна температуре среды. Параметры окружающей среды (воздуха): P ₀=0,1 МПа, t ₀=15ºC. Объем баллона 40 дм³. Воздух считать идеальным газом.

6.14. Определить эксергию воздуха в баллоне. Известны давление и температура воздуха: P =13 МПа, t =200ºC. Параметры окружающей среды: P ₀=0,1 МПа, t ₀=20ºC. Объем баллона 25 дм³. Воздух считать идеальным газом.

6.15. Определить эксергию азота, находящегося в пьезометре экспериментальной установки при P =25 МПа, t =200ºC. Параметры среды: P ₀=0,1 МПа, t ₀=20ºC. Объем пьезометра 500 см³. Азот считать идеальным газом.

6.16. Определить эксергию 100 кДж теплоты при температуре 700ºC. Температура среды 0ºC. Определить потерю эксергии этой теплоты, если последняя будет передана тепловому источнику с температурой 500ºC.

6.17. Определить эксергию количества теплоты, которое получается в результате сгорания на воздухе 1 кг топлива с теплотой сгорания Q _и^p=25,0 МДж/кг; температура горения 1500ºC; температура окружающей среды t ₀=20ºC; теплоемкость продуктов сгорания принять постоянной.

6.18. Для некоторых горячих источников температура газа, выходящего из земли, доходит до 180ºC (давление атмосферное). Определить эксергию 1 кг газа. Температура среды t ₀=20ºC. Считать, что газ по своим термодинамическим свойствам является идеальным и идентичен углекислому газу. Определить максимальный термический к.п.д., который имел бы тепловой двигатель, превращающий теплоту этого источника в работу.

6.19. Определить эксергию 1 кг выходящего из подземных источников водяного пара. Температура пара равна 100ºC, давление атмосферное. Температура окружающей среды 10ºC. Принять, что теплота парообразования r =2257 кДж/кг, а теплоемкость воды с_p =4,187 кДж/(кг·К).

6.20. В сосуде объемом 300 л заключен воздух при давлении P ₁=50 бар и температуре t =20ºC. Параметры среды: P ₀=1 бар, t ₀=20ºC. Определить максимальную полезную работу, которую может произвести сжатый воздух, находящийся в сосуде.

6.21. В сосуде объемом 200 л находится углекислота при температуре t ₁=20ºC и давлении P ₁=100 бар. Температура среды t ₀=20ºC, давление среды P ₀=1 бар. Определить максимальную полезную работу, которую может произвести находящаяся в сосуде углекислота.

6.22. Торпеда приводится в действие и управляется автоматически, двигаясь на заданной глубине. Для двигателя торпеды используется имеющийся в ней запас сжатого воздуха. Определить максимальную полезную работу, которую может произвести воздушный двигатель торпеды, если объем сжатого воздуха в ней V ₁=170 л, давление P ₁=180 бар, а температура воздуха и морской воды t ₀=10ºC. Торпеда отрегулирована на движение под уровнем моря на глубине 4 м. Определить также силу, с которой торпеда устремляется вперед, если радиус ее действия должен быть равен 4 км, а потерями можно пренебречь.

6.23. Определить максимальную полезную работу, которая может быть произведена 1 кг кислорода, если его начальное состояние характеризуется параметрами t ₁=400ºC и P ₁=1 бар, а состояние среды – параметрами t ₀=20ºC, P ₀=1 бар. Представить процесс в диаграммах P-v, T-s.

6.24. В сосуде объемом 400 л заключен воздух при давлении P ₁=1 бар и температуре t ₁= –40⁰C. Параметры среды: t ₀=20ºC, P ₀=1 бар. Определить максимальную полезную работу, которую может произвести воздух, заключенный в сосуд. Представить процесс в диаграммах P-v, T-s.

Дата добавления: 2015-10-29