Равновесная парожидкостная смесь

1. Основным для анализа обратимых термодинамических процессов является уравнение объединенных первого и второго законов (начал) термодинамики в одной из форм (Tds = dq)

dh = Tds + vdP, (7.1)

du = Tds – Pdv. (7.2)

Дополнительно необходимо знать уравнение состояния рабочего вещества (тела), т.е. зависимость, например, вида F (P, v, T)=0. В общем случае, исключая область, где вещество ведет себя как идеальный газ, аналитические выражения для уравнения состояния отсутствуют. Связь между параметрами состояния задается в виде таблиц термодинамических свойств вещества и построенных на их основе P-v-, T-s-, h-s- диаграмм состояния. Это результаты экспериментальных исследований, и для воды они представлены наиболее полно.

2. Качественно P-v- диаграмма имеет вид, представленный на рис. 7.1.

3. Область правее линии FG – область твердого состояния вещества. Для воды, ввиду ее практической несжимаемости, линия FG почти совпадает с изотермой T = 273,15 К = 0ºC.

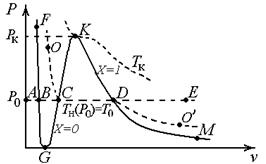
Рис. 7.1. (P, v)-диаграмма состояния вещества:

FGKM – линия фазовых переходов; линия равновесных (насыщенных) состояний вещества;

FG – линия фазового перехода «твердое тело – жидкость»;

GK – линия фазового перехода «жидкость – газ (пар)»; линия начала кипения; нижняя пограничная кривая; линия насыщения жидкости;

KM – линия фазового перехода «пар – жидкость»; линия начала конденсации; верхняя пограничная кривая; линия насыщения пара; сухой насыщенный пар;

точка G – «тройная точка». Для воды это P = 610,8 Па; T = 273,16 К = = 0,01ºC; v = 0,001 м³/кг

Область выше линии FGK – жидкое состояние вещества. Область правее линии KM – газообразное (пар) состояние. В этих областях однофазного состояния термодинамические параметры определяются по соответствующим таблицам или диаграммам состояния. Достаточно задания двух любых параметров состояния (P, v, u, s, h, T).

Замечание 1. При построении таблиц и диаграмм термодинамического состояния воды условно полагается, что u=h=s =0 в тройной точке воды. Поэтому на P-v- диаграмме, например, линия FG совпадает с осью ординат, которая смещается в точку G (рис. 7.1). Значение, например, h _кв критической точке при этом принимает конкретное значение 2095,2 кДж/(кг·К).

4. Область двухфазных состояний расположена ниже кривой GKM. В этой области жидкая и паровая фазы смеси находятся в термодинамически равновесном (насыщенном) состоянии.

Каждому давлению насыщения P = P _н< P _к соответствует строго определенная для каждого простого вещества температура насыщения (T _н), причем зависимость T _н от P _н взаимно однозначная. Соответственно, в двухфазной области равновесных состояний изобара P = P ₀ совпадает с изотермой T = T ₀= T _н (P ₀). (На рис. 7.1 изобара ABCDE (P = P ₀) и изотерма OCDO ¢ (T = T ₀= T _н (P ₀)) имеют общий отрезок CD).

Значения термодинамических параметров состояния (v, u, h, s) каждой из фаз смеси однозначно определяются заданием только давления или температуры T = T _н (P) смеси. В любой точке изобары-изотермы CD их значения для каждой из фаз одни и те же и равны их значениям на пограничных кривых: на нижней (точка С на GK для P = P ₀) для жидкости и на верхней (точка D на KM) для пара. Эти значения находят либо по таблицам свойств жидкости и пара на линии насыщения, либо по таблицам свойств жидкости или пара, где они имеют предельные для каждой фазы значения, либо по соответствующим диаграммам состояний. Параметры жидкости на линии насыщения (нижняя пограничная кривая) будем обозначать одним штрихом вверху (a ¢), а параметры пара на линии насыщения (верхняя пограничная кривая) – двумя штрихами вверху (a ²).

Замечание 2. Задание любого из параметров a ¢ или a ² позволяет по таблицам определить T _н и P _н.

Степень сухости (массовое паросодержание). На изобаре-изотерме термодинамическое состояние каждой из фаз фиксированно и определяется однозначно заданием одного (любого) параметра состояния на линии насыщения (нижней или верхней). Состояние cмеси в точках изобары-изотермы отличаются только массой жидкой (M _ж) и паровой (M _п) фаз смеси при сохранении общей ее массы M = M _ж+ M _п. С подводом энергии жидкость равновесно переходит в пар, с отводом энергии пар переходит в жидкость.

В силу аддитивности (экстенсивности) объема, внутренней энергии, энтальпии и энтропии для любой из удельных массовых величин смеси (v, u, h, s) имеет место равенство

M·a = M _п· a ²+ M _ж· a ¢, M = M _ж+ M _п,

где a – это v, u, h или s.

Отсюда

a = Хa ²+(1– Х) a ¢= a ¢+(a ²– a ¢) Х,(7.3)

где Х= M _п/ M – степень сухости или массовое паросодержание смеси – основной термодинамический параметр парожидкостной смеси в равновесном состоянии.

Из (7.3) следует, что

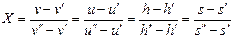. (7.4)

Поскольку задание значения одного из термодинамических параметров a ¢, a ², T _н или P _н определяет значения всех a ¢, a ², то дополнительное задание X или, что то же самое, в силу (7.4) значения одного из термодинамических параметров смеси a полностью определяет все термодинамические параметры парожидкостной смеси (v, u, h, s, P, T).

Из уравнений (7.4) и рис. 7.1 следует:

1) на линии X=X(P) =0 M _п=0 и a = a ¢; это жидкость на линии насыщения – нижняя пограничная кривая GK;

2) на линии X=X(P) =1 M _ж=0 и a = a ²; это пар на линии насыщения в отсутствие жидкой фазы (сухой насыщенный пар) – верхняя пограничная кривая KM;

3) все линии 0< X(P) <1 так же, как X= 0 и X= 1, сходятся в точке K и, не пересекаясь, образуют сетку в двухфазной области. Парожидкостную смесь в этой области называют влажным насыщенным паром. Наличие такой сетки линий X= const на T-s-, h-s -диаграммах позволяет существенно упростить расчеты термодинамических процессов.

Уравнения (7.1), (7.2) на изобаре-изотерме, где P ₀= P _н=const, T ₀ = T _н(P ₀)=const, имеют вид dh = T _н ds, du = T _н ds– P _н dv. Отсюда следует ряд полезных формул:

h ² –h ¢ =T _н(s ² –s ¢) =r (P _н), u ² –u ¢ = r – P _н(v ² –v ¢),

где r – удельная теплота парообразования (Дж/кг), необходимая для перевода 1 кг вещества из состояния «жидкость на линии насыщения» в состояние «сухой насыщенный пар».

h= h ¢+ rX;

s= s ¢+(r / T _н) X;

s ²= s ¢+ r / T _н;

X=(s– s ¢) T _н /r;

X= (h–h ¢)/ r.

(T _н – в кельвинах!)

Замечание 3. Значения X, определяемые по формулам (7.4), являются степенью сухости M _п/ M только при 0£ X £1. Если X <0, это значит только, что вещество в жидком состоянии (недогретая до кипения жидкость). Если X >1 – вещество в газообразном состоянии (пар), причем его температура выше температуры насыщения (сухой перегретый пар).

Дата добавления: 2015-10-29