
Читайте также:
|
Исследование термодинамического процесса включает в себя получение аналитической связи между термодинамическими параметрами газа, определение их значений и приращений в различных термодинамических состояниях, реализуемых в процессе.
Фундаментальные соотношения для идеального газа (в удельных массовых величинах):
Pv = RT – уравнение состояния (Клапейрона);
du = cvdT, dh = cpdT – закон Джоуля;
|
|
|
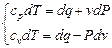 –
–
Изобарный процесс (P = P 0=const)
а). В этом случае для любых двух состояний газа
P 0 v 1= RT 1, P 0 v 2= RT 2.
Отсюда следует характерная для этого процесса связь между термодинамическими параметрами (уравнение процесса):
 или
или 
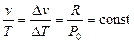 .
.
б). Поскольку dP º0, то из (5.1) следует, что все тепло идет на изменение энтальпии:
D q = D h = cpdT.
Располагаемая работа равна нулю.
в). С учетом этого из (5.2) следует
D u = D h – P 0D V = D h – R D T.
Работа расширения D А = P 0D V.
Изохорный процесс (V = V 0=const)
Поскольку M =const, то v 0= V 0/ M =const.
a). Для любых двух состояний
P 1 v 0= RT 1 , P 2 v 0= RT 2.
Отсюда следует уравнение изохорного процесса
 или
или 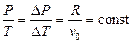 .
.
б). Из (5.2) получаем D q =D u = cv D T – все тепло идет на изменение внутренней энергии; т.к. dv º0, работа расширения равна нулю.
в). Из (5.1) следует
D h = D u +v 0D P = D u+R D T = D q+v 0D P.
Располагаемая работа v 0D P = D h –D u = R D T.
Изотермический процесс (T = T 0=const)
а). Из уравнения состояния для двух произвольных «точек» этого процесса
P 1 v 1= RT 0 , P 2 v 2= RT 0
следует уравнение процесса
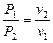 или Pv = RT 0=const.
или Pv = RT 0=const.
б). В соответствии с законом Джоуля, т.к. dT º0,
du = cvdT º 0, dh = cpdT º 0 (D u =D h =0).
в). Из уравнения (5.2) следует, что dq = Pdv – все тепло идет на совершение работы, и наоборот.
Из (5.1) следует, что dq = –vdP – располагаемая работа равна работе расширения с обратным знаком.
г). Произведенная работа (работа расширения)

Здесь использованы следующие из уравнения процесса равенства:
P 1 v 1= P 2 v 2 = Pv = RT 0=constи 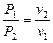 .
.
Адиабатный процесс (dq= 0)
В этом процессе отсутствует теплообмен с окружающей средой:
D Q = M D q =0.
a).Поскольку dq= 0, уравнения (5.1), (5.2) имеют вид
 ,
, 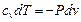 (
(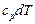 = dh;
= dh;  = du).
= du).
Разделив первое уравнение на второе (отдельно левые и правые части), получаем
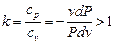
( – показатель адиабаты). Из этого уравнения следует
– показатель адиабаты). Из этого уравнения следует 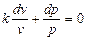 , т.е.
, т.е.  ,
, 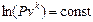 и
и
 или
или 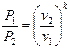 . (5.3)
. (5.3)
Это и есть уравнение адиабатного процесса, а т.к. Pv = RT, можно представить его в виде
 или
или 
 . (5.4)
. (5.4)
б). Располагаемая работа в адиабатном процессе в k раз больше работы расширения:
vdP = – k (Pdv).
Поскольку vdP = dh, а du = – pdv, приращение энтальпии в k раз больше приращения внутренней энергии:
dh=kdu.
в). Для работы (работа расширения), совершаемой газом в адиабатном процессе при переходе из одного состояние в другое,
dA=Pdv.
Поскольку h = u + Pv, то
dh–du=d(Pv)=Pdv+vdP=dA–kdA=( 1 –k)dA,
следовательно, получаем
dA= –d(Pv)/(k– 1 ).
Отсюда после интегрирования
 .
.
Используя различные уравнения адиабатного процесса (5.3) или (5.4), формулам для D A можно придать различный вид, например,
 .
.
Политропный процесс (dq = c п dT, c п=const)
Этот процесс характеризуется линейной зависимостью D Q от T.
а). Для этого процесса уравнения (5.1), (5.2) имеют вид
 (du = cvdT, dh = cpdT),
(du = cvdT, dh = cpdT), 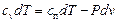 .
.
Перенесем  в левые части этих уравнений:
в левые части этих уравнений:
 ,
,
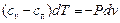 .
.
Разделив первое уравнение на второе, получим
 , vdP = – n (Pdv)= – ndA
, vdP = – n (Pdv)= – ndA
(n – показатель политропы). Действуя как в предыдущем пункте, получим уравнение политропного процесса

или

т.е. уравнения предыдущего пункта (5.3) и (5.4) с заменой k на n.
Замечание. Из равенства  c учетом того, что cp=kcv, следует связь между n и k:
c учетом того, что cp=kcv, следует связь между n и k:
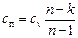 .
.
б). Для работы, совершаемой газом (dA=Pdv) при переходе из одного состояния в другое, получаем те же формулы, что и для адиабатного процесса, с заменой в них k на n. Действительно,
dh–du=d (Pv) =Pdv+vdP=–ndA+kdA= (1 –n) dA
и
dA= –d(Pv)/(n–1).
Отсюда

и т.д.
Замечание. Задание объема V н (м3) идеального газа, «приведенного к нормальным условиям» (P 0=101325 Па, T 0=273,15 К), фактически задает его массу M (кг), т.к.
P 0 V н= МRT 0.
Дата добавления: 2015-10-29; просмотров: 266 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример решения задач | | | Пример решения задач |