Графическое определение коэффициента перекрытия

где - коэффициент перекрытия (см. п. 2.3),

- коэффициент перекрытия полученный построением,

- линия зацепления с чертежа.

Рb=25.12мм - шаг с чертежа.

Вывод

1. Произведен расчет эвольвентного зубчатого зацепления, выбран коэффициент смещения , удовлетворяющий качественным показателям передачи и обеспечивающий отсутствие подреза и заострения.

2. Построено эвольвентное зацепление.

3. Построено станочное зацепление.

Произведено графическое определение коэффициента перекрытия , погрешность 1.8%.

Проектирование планетарного редуктора

Исходные данные и постановка задачи

- схема механизма – однорядный планетарный редуктор со смешанным зацепление;

- все колеса имеют одинаковый модуль m=1мм;

- число сателлитов планетарного редуктора k=3;

- передаточное отношение U=3.39;

Необходимо:

- спроектировать планетарный редуктор, удовлетворяющий всем условиям, накладываемым на многосателитный редуктор;

- начертить схему редуктора в масштабе;

- выполнить проверку передаточного отношения графически;

Основные условия проектирования многосателитного планетарного редуктора

(Рассматриваемые ниже условия диктуются наличием нескольких сателлитов)

1. Формула Виллиса.

Передаточное отношение планетарного редуктора от солнечного колеса к водилу равно 1 минус передаточное отношение обращенного механизма от солнечного колеса к опорному.

2. Условие соосности входного и выходного валов механизма, т.е. межосевое расстояние первой передачи должно быть равно межосевому расстоянию второй передачи .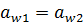

3. Условия сборки с симметрией зон зацепления, т.е. условия размещения сателлитов с равными углами между их осями (). Математически это условие может быть записано так:

где К-число сателлитов,

P-целое число полных оборотов водила,

N-любое отвлеченное целое число.

4. Условие совместимости или соседства, которое учитывает возможность свободного размещения сателлитов без соприкосновения их друг с другом. Это условие будет выполнено, если расстояние между осями сателлитов будет больше диаметра окружности вершин сателлитов .

Математически это условие для механизмов записывается неравенством:

.

Подбор чисел зубьев планетарного редуктора

Передаточное отношение планетарного редуктора:

Схема механизма:

При подборе чисел зубьев учитываются ограничения накладываемые отсутствием подреза:

; внутреннее зацепление малое колесо

; внутреннее зацепление большое колесо

; внешнее зацепление

Т.е. для однорядного планетарного редуктора со смешенным зацеплением

; ;

Подберем число зубьев, учитывая все условия, накладываемые на многосателлитные редукторы:

1. Формула Виллиса: ;

2. Условие соосности: ;

3. Условие сборки: ;

4. Условие совместимости: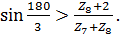

При P=33 Z₇ – любое целое цисло.

Число зубьев находим перебором. Первое условие: Z₇ должно быть больше 17. Второе условие Z₉ должно быть больше 85, используя формулу Виллиса получаем выражение для Z₉=U_1в-1*Z₇. Таким образом находим пару чисел 40 и 96. Пара подходит и получаем, что Z₈=28.0,

Z₇=40, Z₈=28, Z₉=96.

Проверка условия соосности:

40+28=96-28; 68=68; верно.

Проверка условия совместимости:

верно.

В результате расчета подобраны числа зубьев колес однорядного планетарного редуктора со смешанным зацеплением, удовлетворяющие всем условиям. Накладываемым на многосателлитные редукторы:

Z₇=40, Z₈=28, Z₉=96.

Дата добавления: 2015-10-26