Читайте также:
|
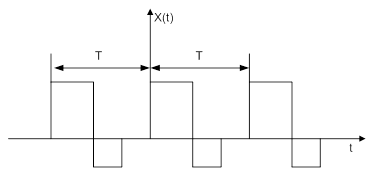
Непериодический сигнал можно представить как частный случай периодического сигнала, при условии, что период сигнала стремится к бесконечности.
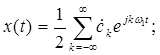(0)
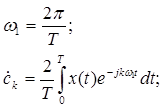
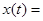
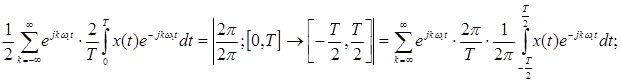
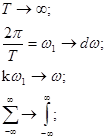
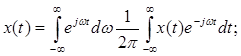
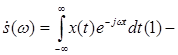спектральная плотность амплитуд.
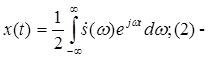интеграл Фурье.
Формула (1) называется прямым преобразованием Фурье, а формула (2) обратным преобразованием Фурье.
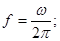
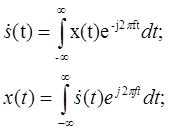
Сравнивая формулы (2) и (0) можно записать:
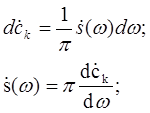
Это амплитуда, приходящаяся на узкую полосу частот.
Перепишем (1) в виде:
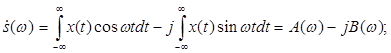
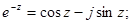
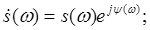
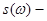модуль спектральной плотности.
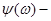аргумент спектральной плотности.
и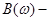 
вещественная и мнимая часть комплексной функции.
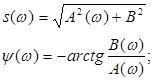
Рассмотрим по (3) формуле два случая:
1.x(t)-четная функция.
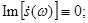Спектральная плотность чисто вещественная.
2.x(t)-нечетная функция.
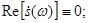Спектральная плотность чисто мнимая.
Пусть мнимая часть сигнала x(t)=0.
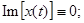
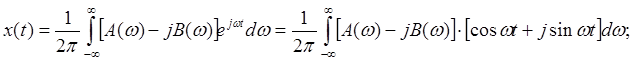
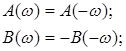
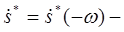комплексно сопряженные функции.
Дата добавления: 2015-09-04; просмотров: 90 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Классификация и модели биомедицинских сигналов | | | Круговой сдвиг последовательности. |