Читайте также:
|
1. 
.
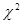Рассмотрим n независимых случайных величин: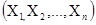 
,- каждая из которых подчиняется нормальному распределению.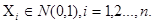 
Образуем новую случайную величину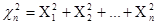 
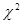- это с n степенями свободы(кол-во случ величин, входящих в хи квадрат, каждая из которых распределена нормально с нулевым мат ожиданием и единичной дисперсией).
Существуют таблицы квантилей этого распределения.
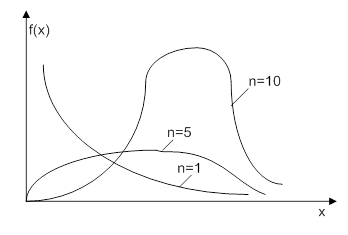
Можно утверждать, что при n>30 распределение 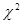можно считать нормальным.
2. Распределение Стьюдента.
Пусть Y и Z независимые случайные величины, причем Y принадлежит распределению 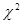, а Z – нормальному распределению.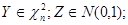 
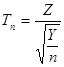- коэффициент Стьюдента с n степенями свободы.
Существует таблица квантилей этого распределения.
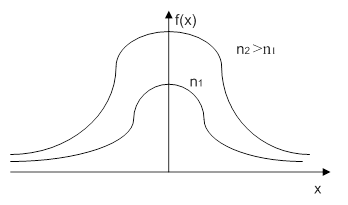
Можно утверждать, что при n>30 распределение Стьюдента совпадает с нормальным.
3. Распределение Фишера
Пусть Y 1, Y 2 — две независимые случайные величины, имеющие распределение хи-квадрат: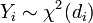 
, где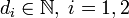 
. Тогда распределение случайной величины
,
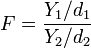называется распределением Фишера (распределением Снедекора) со степенями свободы d 1 и d 2. Пишут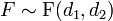 
.
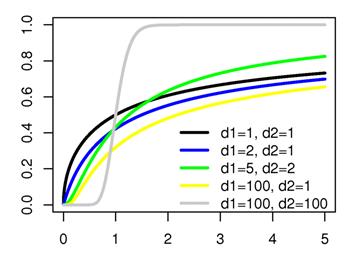
Теорема Фишера
Для выборки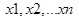 
объема n нормальной ГС Х с параметрами 
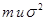т.е.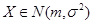 
выборочная средняя
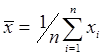и выборочная дисперсия
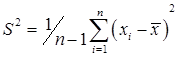
статистически независимы. Причем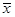 
распределена нормально с параметрами 
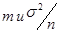, а величина
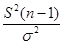имеет распределение 
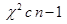степенями свободы, т.е.
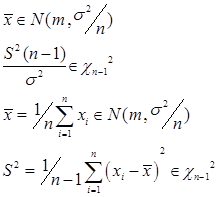
2 Круговой сдвиг последовательности. Круговая свёртка
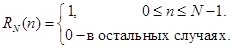
Изобразим на рисунке следующие 4 последовательности:
Сравнение показывает, что x1(n) – не соответствует линейному сдвигу x(n).
Для трактовки такого сдвига представим, что последовательность конечной длины x(n) расположена на поверхности цилиндра в N точках. При движении по поверхности цилиндра наблюдаемая последовательность будет периодической последовательностью x̃(n). При этом линейный сдвиг последовательности x̃(n) соответствует вращению цилиндра. Такой сдвиг называется круговым.
Дата добавления: 2015-09-04; просмотров: 88 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Передаточная функция цифровых ЛИВ систем | | | Круговая свертка. |