Читайте также:
|
z-преобразование 
определяется следующим образом 
z=a+jb=zejw
zпреобразование - это преобразование Фурье численной последовательности, умноженной на z-n(на модуль комплексной переменной)
при zпо модулю = 1 zпреобр-е переходит в преобр-е Фурье
Условия существования z-преобразования:
Абсолютное суммирование последовательности: 
.
Важный класс z-преобразований составляют те, которые являются рациональными функциями, т.е. отношениями полиномов: 
Корни полинома числителя называются нулями z-преобразований. Корни полинома знаменателя называют полюсами.
Ясно, что в области сходимости полюсов не должно быть. Область сходимости ограничивается полюсами.
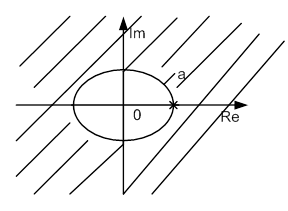
Рассмотрим пример:
Нули: z=0; Полюс: z=a.
Теоремы о z-преобразованиях:
1. Линейность. 
2.Сдвиг последовательности:
3. Свертка последовательностей: Образуем последовательность ω(n), как свертку двух последовательностей:
Z-преобразование совпадает с преобразованием Фурье на единичной окружности. В общем случае степенной ряд 1 Лорана будет сходиться в кольцевой области z-плоскости.
Дата добавления: 2015-09-04; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Эффект наложения спектров. Частота Найквиста | | | Обратное z-преобразование |