Обратное z-преобразование

Обратное z-преобразование выводится на основе теоремы Каши:

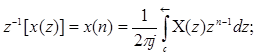
С – это контур с направлением обхода против часовой стрелки расположенный в области сходимости x(t) и окружающий начало координат.

Если 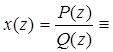рациональная функция, то значение интеграла удобно вычислять с помощью теоремы о вычетах:

.

Представим:

Z0 – полюс порядка s, а ψ (z) не имеет полюсов в точке z=z0.

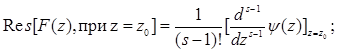
Частный случай: s=1.

Пример

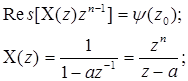
Пусть n=-1

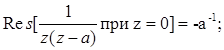
второй полюс

Существуют таблицы прямого и обратного преобразования. Удобно представить рациональную функцию в виде степенного ряда:

;

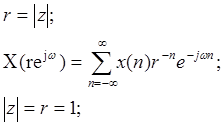
Дата добавления: 2015-09-04