Читайте также:
|
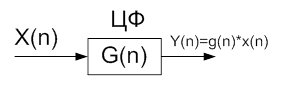
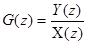- передаточная функция фильтра.
В общем случае для устойчивого и физически реализуемого ЦФ область сходимости передаточной функции будет включать единичную окружность и всю z-плоскость вне окружности, включая z=∞.
Область сходимости не содержит полюсов, значит для устойчивости надо, чтобы все полюса передаточной функции лежали внутри окружности 
Как известно ЦФ описывается разностным уравнением n-го порядка:
Воспользуемся свойством линейности:
Воспользуемся свойством сдвига последовательности:
Рассмотрим пример:
Пусть необходим ЦФ не пропускающий постоянную составляющую.
Возьмем z-преобразование от левой и правой части равенства:
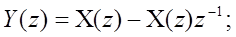
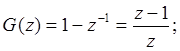
Дата добавления: 2015-09-04; просмотров: 95 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Обратное z-преобразование | | | Распределения, связанные с нормальным |