Интеграл ауманна

Определение 5. Многозначным отображением будем называть произвольную функцию то есть функцию, аргументом которой является время а значениями – элементы пространства то есть непустые компактные множества из

Так как пространства и метрические, то можно говорить о непрерывности многозначного отображения.

Определение 6. Многозначное отображение непрерывно в точке если для любого существует такое, что при всех удовлетворяющих условию справедливо неравенство

По определению расстояния по Хаусдорфу это означает, что многозначное отображение непрерывно в точке если для любого существует такое, что при всех удовлетворяющих условию выполняются одновременно следующие два включения

В случае, когда выполняется лишь первое включение, многозначное отображение называется полунепрерывным сверху в точке Если же выполняется второе включение, то многозначное отображение называется полунепрерывным снизу в точке Таким образом, многозначное отображение непрерывно в точке тогда и только тогда, когда оно полунепрерывно сверху и снизу в данной точке.

Определение 7. Многозначное отображение назовем непрерывным на отрезке 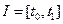, если оно непрерывно в каждой точке этого отрезка.

Теорема 1 [Благодатских]. Пусть 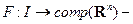непрерывное многозначное отображение. Тогда опорная функция непрерывна по при каждом фиксированном значении Наоборот, если функция непрерывна по при каждом фиксированном значении то многозначное отображение непрерывно.

Следствие 11. Многозначное отображение непрерывно тогда и только тогда, когда опорная функция непрерывна по при каждом фиксированном значении

Определение 8. Многозначное отображение назовем измеримым на отрезке если его опорная функция измерима по на отрезке для каждого фиксированного вектора

Такое определение измеримости является очень общим, и широ­кий класс отображений измерим в указанном смысле. Обычно в литературе по многозначным отображениям измеримость опреде­ляют для более узкого класса отображений Поскольку по опорной функции можно восстановить лишь выпук­лую оболочку данное определение измеримости накла­дывает ограничение на поведение лишь многозначного отображения и никак не отражает того, что происходит с той частью множества которая лежит внутри Тем не менее все приводимые ниже результаты справедливы для многозначных отображений измеримых в указанном смысле.

Любое непрерывное многозначное отображение измеримо, поскольку его опорная функция непрерывна по при каждом фиксированном и, следовательно, измерима.

Определение 9. Функция называется однозначной ветвью многозначного отображения если при всех выполняется включение

Ясно, что однозначная ветвь всегда существует, поскольку множество непусто при всех

Теорема 2 (теорема А.Ф.Филиппова) [ ]. Если многозначное ото­бражение измеримо, то у него существует измеримая однозначная ветвь

Пусть заданы отрезок времени 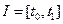и некоторое отображение

Определение 10 [Aumann]. Интегралом Ауманна от многозначного отображения на отрезке называется множество

Здесь в правой части интеграл Лебега берется по всем однозначным ветвям отображения для которых он существует. Ясно, что является подмножеством пространства

Теорема 3 (теорема А.А.Ляпунова) [ ]. Пусть многозначное отображение измеримо на отрезке и где 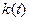суммируема на Тогда интеграл от этого многозначного отображения является непустым выпуклым компактным множеством в пространстве то есть

Следствие 12. Пусть многозначное отображение непрерывно на отрезке Тогда

Пример 6. Рассмотрим многозначное отображение Найдем интеграл

Очевидно, что максимальное значение равно 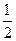и достигается на непрерывной однозначной ветви Минимальное значение равно и достигается на непрерывной однозначной ветви 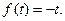Таким образом,

Пусть произвольная точка отрезка 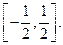Покажем, что существует однозначная ветвь многозначного отображения такая, что интеграл Лебега Такая ветвь будет уже разрывной, например,

Действительно, функция интегрируема по Лебегу и

Это означает, что Следовательно,

Теорема 4 [Благодатских]. Пусть многозначное отображение измеримо на отрезке и где 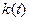суммируема на Тогда имеет место равенство

Следствие 4. Пусть многозначное отображение непрерывно на отрезке Тогда имеет место равенство.

С помощью данной теоремы можно довольно просто находить интегралы от многозначных отображений Действительно, для этого достаточно в соответствии с формулой построить опорную функцию проинтегрировать уже однозначную функцию по при каждом значении а затем восстановить по полученной опорной функции непустое выпуклое компактное множество Заметим, что для восстановления выпуклого множества достаточно подобрать такое множество , чтобы его опорная функция совпадала с 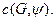Тогда согласно следствию 6 из свойства 11 опорных функций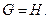

Пример 7. Найти интеграл от многозначного отображения

В силу теоремы 4 имеем

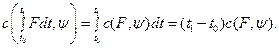
Такую же опорную функцию имеет выпуклое компактное множество так как в силу свойств 5 и 7 опорной функции имеем

Таким образом,

Пример 8. Вычислить интеграл от многозначного отображения на отрезке

Решение. Для построения множества найдем его опорную функцию, воспользовавшись теоремой 4:

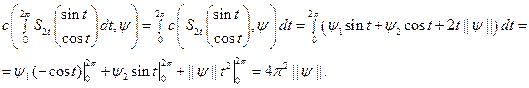
Опорная функция шара также имеет вид то есть опорные функции множеств и совпадают. Следовательно, в силу следствия 6 из свойства 11 опорных функций

Ответ: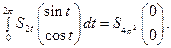

Пример 9. Вычислить интеграл от многозначного отображения 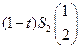на отрезке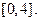

Решение. Для построения множества найдем его опорную функцию, воспользовавшись теоремой 4:

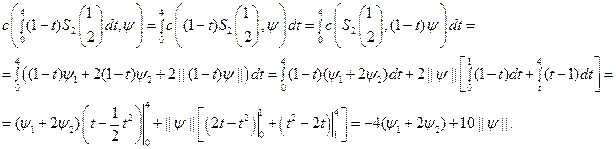
Опорная функция шара также имеет вид то есть опорные функции множеств и совпадают. Следовательно, в силу следствия 6 из свойства 11 опорных функций

Ответ:

Пример 10. Вычислить интеграл от многозначного отображения 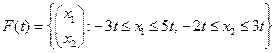на отрезке

Решение. Для построения множества найдем его опорную функцию, воспользовавшись теоремой 4:

Опорная функция прямоугольника также имеет вид то есть

Ответ: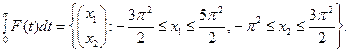

Пример 11. Вычислить интеграл от многозначного отображения на отрезке

Решение. Найдем опорную функцию множества

Так как и то существует такое, что Тогда

В силу π – периодичности функции имеем

Опорная функция шара 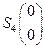также имеет вид то есть

Ответ: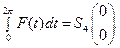

Пример 12. Вычислить интеграл от многозначного отображения на отрезке

Решение. Найдем опорную функцию множества

Опорная функция квадрата также имеет вид поэтому

Ответ:

Пример 13. Вычислить интеграл от многозначного отображения на отрезке

Решение. Найдем опорную функцию множества

Найдем новый опорный вектор и его модуль: Тогда

Опорная функция шара 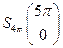также имеет вид поэтому

Ответ:

Дата добавления: 2015-09-05