
Читайте также:
|
1. Опорная функция 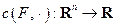 положительно однородна, то есть
положительно однородна, то есть

для любого вектора  и любого числа
и любого числа  . В частности,
. В частности,  .
.
2. Для любых двух векторов  опорная функция удовлетворяет неравенству
опорная функция удовлетворяет неравенству

Следствие 1. Опорная функция 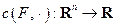 является выпуклой.
является выпуклой.
3. Пусть  Тогда опорная функция
Тогда опорная функция  суммы
суммы  равняется сумме двух опорных функций
равняется сумме двух опорных функций  и
и 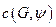 , то есть
, то есть

4. Пусть  - матрица размером
- матрица размером 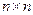 , а
, а  Тогда
Тогда

где 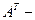 матрица, транспонированная к матрице А.
матрица, транспонированная к матрице А.
5. Пусть  a
a  произвольное число. Тогда
произвольное число. Тогда

Следствие 2. Опорная функция  положительно однородна по первому аргументу
положительно однородна по первому аргументу  , то есть
, то есть  для любого числа
для любого числа  .
.
6. Пусть  Если выполняется включение
Если выполняется включение 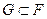 , то для любого вектора
, то для любого вектора  справедливо неравенство
справедливо неравенство

Следствие 3. Пусть  Если точка
Если точка 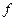 принадлежит множеству
принадлежит множеству  , то для любого вектора
, то для любого вектора  выполняется неравенство
выполняется неравенство 
7. Пусть  Тогда опорные функции множеств
Тогда опорные функции множеств  и
и  совпадают, то есть
совпадают, то есть

8. Пусть заданы множество 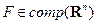 и его опорная функция
и его опорная функция  . Тогда выпуклая оболочка
. Тогда выпуклая оболочка  множества
множества  представляется в виде
представляется в виде

Здесь и далее S – единичная сфера с центром в начале координат.
9. Пусть 
 Если для любого вектора
Если для любого вектора  выполняется неравенство
выполняется неравенство

то точка 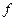 принадлежит выпуклой оболочке
принадлежит выпуклой оболочке  множества
множества 
Следствие 4. Пусть множество  В таком случае точка
В таком случае точка 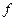 принадлежит множеству
принадлежит множеству  тогда и только тогда, когда неравенство выполняется для любого вектора
тогда и только тогда, когда неравенство выполняется для любого вектора  .
.
10. Пусть  Если для любого вектора
Если для любого вектора  выполняется неравенство
выполняется неравенство

то справедливо включение GÌ coF.
Следствие 5. Пусть  и множество
и множество  выпукло. Тогда включение
выпукло. Тогда включение  справедливо тогда и только тогда, когда для любого вектора
справедливо тогда и только тогда, когда для любого вектора  выполняется неравенство (8).
выполняется неравенство (8).
11. Пусть  Если множества
Если множества  и
и  равны, то их опорные функции совпадают. Наоборот, если их опорные функции совпадают, то
равны, то их опорные функции совпадают. Наоборот, если их опорные функции совпадают, то 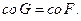
Следствие 6. Множества  равны тогда и только тогда, когда их опорные функции совпадают. Таким образом, множество
равны тогда и только тогда, когда их опорные функции совпадают. Таким образом, множество  можно однозначно восстановить по его опорной функции
можно однозначно восстановить по его опорной функции  .
.
12. Пусть  . Если множества
. Если множества  и
и  пересекаются, то есть
пересекаются, то есть  , то для любого вектора
, то для любого вектора  выполняется неравенство
выполняется неравенство

Наоборот, если выполняется соотношение для любого вектора  , то
, то 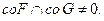
Следствие 7. Два множества  пересекаются тогда и только тогда, когда неравенство выполняется для любого вектора
пересекаются тогда и только тогда, когда неравенство выполняется для любого вектора  .
.
13. Опорная функция  для любых двух множеств
для любых двух множеств  и любых двух векторов
и любых двух векторов  удовлетворяет неравенству
удовлетворяет неравенству
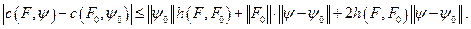
Следствие 8. Опорная функция  непрерывна по совокупности переменных
непрерывна по совокупности переменных  в любой точке
в любой точке  и, следовательно, непрерывна по каждой из переменных
и, следовательно, непрерывна по каждой из переменных  в отдельности.
в отдельности.
14. Пусть  Если точка
Если точка 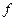 является внутренней точкой множества
является внутренней точкой множества  , то для любого вектора
, то для любого вектора  выполняется неравенство
выполняется неравенство

Наоборот, если соотношение выполняется для любого вектора  , то
, то 
Следствие 9. Точка 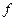 принадлежит внутренности множества
принадлежит внутренности множества 
 тогда и только тогда, когда неравенство справедливо для любого вектора
тогда и только тогда, когда неравенство справедливо для любого вектора  .
.
15. Пусть заданы два множества  Тогда справедливо соотношение
Тогда справедливо соотношение

Следствие 10. Для множеств  справедливо равенство
справедливо равенство

Заметим, что если множества  не являются выпуклыми, то в формуле может быть строгое неравенство.
не являются выпуклыми, то в формуле может быть строгое неравенство.
Дата добавления: 2015-09-05; просмотров: 151 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ОПОРНАЯ ФУНКЦИЯ И ЕЕ ОСНОВНЫЕ СВОЙСТВА | | | Пример 5. |