Опорная функция и ее основные свойства

Определение 4. Пусть задано некоторое множество Опорной функцией множества называется скалярная функция векторного аргумента определяемая условием

Множество также считается одним из аргументов функции . Зафиксируем множество . Функция как функция аргумента 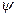отображает пространство в числовую ось Максимум в правой части равенства достигается, так как скалярное произведение 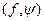непрерывно по 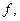а множество компактно.

Пусть некоторый фик­сированный вектор, а один из векторов множества , на котором достигается максимум в определении опорной функции для вектора , то есть выполняется равенство

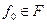В этом случае вектор называется опорным вектором к множеству в точке , а совокупность всех векторов , удовлетворяющих равенству, называется опорным множеством к множеству в направлении вектора 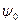. Гиперплоскость в пространстве определяемая соотношением

называется опорной гиперплоскостью к множеству в направ­лении вектора

Для опорного множества справедливо представление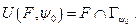

Гиперплоскость разбивает все пространство на два полупространства и Множество лежит в отрицательном полупространстве относительно вектора 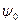, так как для всех точек 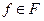выполняется неравенство

Дата добавления: 2015-09-05