
Читайте также:
|
Пусть  и матрица A имеет вид
и матрица A имеет вид

Легко показать, что единичный шар 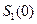 при таком линейном преобразовании перейдет в эллипс
при таком линейном преобразовании перейдет в эллипс

если 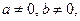 или в отрезок
или в отрезок
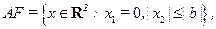
если 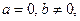 или в отрезок
или в отрезок

если  или в точку
или в точку  если
если 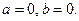
В пространстве  можно ввести метрику, или расстояние, между двумя множествами
можно ввести метрику, или расстояние, между двумя множествами  и
и  по формуле:
по формуле:

Таким образом, расстоянием между двумя множествами является наименьшее из положительных чисел  , для которых выполняются одновременно два включения
, для которых выполняются одновременно два включения  ,
,  . Эта метрика называется хаусдорфовой.
. Эта метрика называется хаусдорфовой.
Легко проверить, что 
Пример 4. Найти расстояние по Хаусдорфу между множествами F и G, изображенными на рисунке:
1)
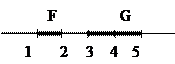
| Используя определение расстояние по Хаусдорфу и рассмотренные примеры нахождения суммы множеств, получаем, что  при при   при при 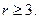 Таким образом, h(F,G)=3. Таким образом, h(F,G)=3.
|
2)

|  при при   при при 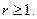 Таким образом, h(F,G)=1. Таким образом, h(F,G)=1.
|
3)
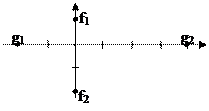
|  при при   при при  Таким образом, h(F,G)= Таким образом, h(F,G)= 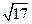 . .
|
4)

|  при при 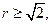  при при 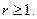 Таким образом, h(F,G)= Таким образом, h(F,G)= 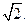
|
5)

|  при при 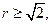  при при 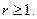 Таким образом, h(F,G)= Таким образом, h(F,G)= 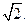
|
6)

|  при при   при при 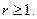 Таким образом, h(F,G)= 3.
Таким образом, h(F,G)= 3.
|
7)

|  при при   при при  Таким образом, h(F,G)= 3. Таким образом, h(F,G)= 3.
|
8)
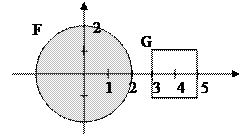
|  при при   при
при  Таким образом, h(F,G)= 5.
Таким образом, h(F,G)= 5.
|
Дата добавления: 2015-09-05; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Лінійні задачі керування | | | ОПОРНАЯ ФУНКЦИЯ И ЕЕ ОСНОВНЫЕ СВОЙСТВА |