
Читайте также:
|
Рассмотрим объект, движение которого описывается линейной системой дифференциальных уравнений

где  время,
время,  фазовый вектор,
фазовый вектор,  вектор управления,
вектор управления,  матрица размера
матрица размера 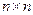 с вещественными элементами.
с вещественными элементами.
Пусть задано множество 
Определение 11. Функция 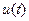 называется допустимым управлением на некотором отрезке
называется допустимым управлением на некотором отрезке  если она измерима и удовлетворяет включению
если она измерима и удовлетворяет включению  для всех
для всех 
Пусть в пространстве  заданы два непустых компактных множества
заданы два непустых компактных множества  и
и  Будем говорить, что допустимое управление
Будем говорить, что допустимое управление 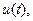 заданное на отрезке
заданное на отрезке  осуществляет переход объекта из начального множества
осуществляет переход объекта из начального множества  на конечное множество
на конечное множество  если соответствующее решение системы
если соответствующее решение системы

удовлетворяет граничным условиям

В дальнейшем будем предполагать, что начальный момент времени  зафиксирован, а конечный момент
зафиксирован, а конечный момент 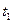 определяется из условия попадания решения
определяется из условия попадания решения  на множество
на множество 
Задача быстродействия заключается в нахождении допустимого управления 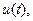 осуществляющего переход из множества
осуществляющего переход из множества  на множество
на множество  за наименьшее время.
за наименьшее время.
Теорема (о существовании оптимального управления) [Благодатских В.И.]. Пусть существует хотя бы одно допустимое управление 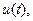 осуществляющее переход объекта из начального множества
осуществляющее переход объекта из начального множества  на конечное множество
на конечное множество  Тогда существует оптимальное управление
Тогда существует оптимальное управление  переводящее объект из множества
переводящее объект из множества  на множество
на множество  за минимальное время
за минимальное время
Определение 12 [Благодатских]. Будем говорить, что пара  удовлетворяет принципу максимума Понтрягина на отрезке времени
удовлетворяет принципу максимума Понтрягина на отрезке времени  если существует такое решение
если существует такое решение  вспомогательной сопряженной системы дифференциальных уравнений
вспомогательной сопряженной системы дифференциальных уравнений

с начальным условием  что выполнены следующие условия:
что выполнены следующие условия:
а) условие максимума:

для почти всех 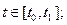
б) условие трансверсальности на множестве 

в) условие трансверсальности на множестве 

Теорема (необходимые условия оптимальности) [Благодатских В.И.]. Пусть в задаче быстродействия множества  и
и  выпуклы. Пусть, далее,
выпуклы. Пусть, далее,  оптимальное управление, переводящее объект из множества
оптимальное управление, переводящее объект из множества  на множество
на множество  на отрезке времени
на отрезке времени 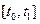 и
и  соответствующее ему решение системы. Тогда пара
соответствующее ему решение системы. Тогда пара  удовлетворяет принципу максимума Понтрягина на отрезке времени
удовлетворяет принципу максимума Понтрягина на отрезке времени 
Таким образом, для решения задачи быстродействия можно поступить следующим образом: найти все управления, удовлетворяющие принципу максимума Понтрягина, а затем среди этого множества управлений каким-либо образом найти действительно оптимальное управление. Эффективность такого подхода определяется тем, как много управлений будет удовлетворять принципу максимума. Чем уже множество таких управлений, тем проще выбрать из него действительно оптимальное управление. Оказывается, что принцип максимума Понтрягина в этом смысле является довольно эффективным средством решения линейных задач быстродействия.
Рассмотрим, как построить все управления, удовлетворяющие принципу максимума. Для этого можно предложить следующую схему (рис. 1). Начальный момент времени  в нашей задаче зафиксирован. Возьмем произвольный начальный вектор
в нашей задаче зафиксирован. Возьмем произвольный начальный вектор  из единичной сферы
из единичной сферы  Найдем решение
Найдем решение  сопряженной системы с этим начальным значением
сопряженной системы с этим начальным значением  В силу теоремы Каратеодори это решение
В силу теоремы Каратеодори это решение  [Филиппов] существует и единственно на любом отрезке времени
[Филиппов] существует и единственно на любом отрезке времени 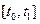 и определяется формулой Коши
и определяется формулой Коши

Факт единственности этого решения показан на схеме одинарной стрелкой. Далее, зная решение  сопряженной системы, найдем все допустимые управления
сопряженной системы, найдем все допустимые управления  удовлетворяющие условию максимума. Таких управлений
удовлетворяющие условию максимума. Таких управлений 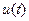 может быть несколько, и это указано на схеме двойной стрелкой.
может быть несколько, и это указано на схеме двойной стрелкой.
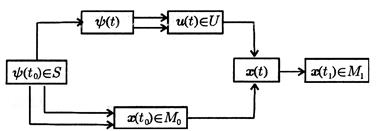
Рис. 1
По данному же начальному вектору  найдем все начальные значения вектора фазового состояния объекта
найдем все начальные значения вектора фазового состояния объекта  из начального множества
из начального множества  удовлетворяющие условию трансверсальности на множестве
удовлетворяющие условию трансверсальности на множестве  . Таких начальных значений
. Таких начальных значений  опять может быть несколько. Этот факт также показан на схеме двойной стрелкой. Теперь, зная допустимое управление
опять может быть несколько. Этот факт также показан на схеме двойной стрелкой. Теперь, зная допустимое управление 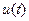 и начальное состояние объекта
и начальное состояние объекта  найдем решение уравнения. Это решение
найдем решение уравнения. Это решение  в силу теоремы Каратеодори существует, единственно и определяется формулой Коши
в силу теоремы Каратеодори существует, единственно и определяется формулой Коши

После того, как построено решение  осталось только проверить, достигнет ли это решение при каком - либо
осталось только проверить, достигнет ли это решение при каком - либо  множества
множества  или нет, а если решение
или нет, а если решение  достигнет в какой - то момент
достигнет в какой - то момент 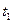 множества
множества  то выполняется ли условие трансверсальности на множестве
то выполняется ли условие трансверсальности на множестве  . Если это условие выполнено, то пара
. Если это условие выполнено, то пара  удовлетворяет принципу максимума Понтрягина на полученном отрезке времени
удовлетворяет принципу максимума Понтрягина на полученном отрезке времени  если это условие не выполнено, то пара
если это условие не выполнено, то пара  не удовлетворяет принципу максимума.
не удовлетворяет принципу максимума.
Заметим, что при таком подходе все пары  удовлетворяющие принципу максимума, зависят лишь от начального вектора
удовлетворяющие принципу максимума, зависят лишь от начального вектора  причем эта зависимость на двух этапах может быть неоднозначной.
причем эта зависимость на двух этапах может быть неоднозначной.
Проиллюстрируем данную схему решения задачи быстродействия на конкретных примерах.
Пример 14. Решить задачу быстродействия







Рис.2
Решение. Не ограничивая общности, будем считать, что  Приведем данную задачу к стандартному виду. Для этого введем новые переменные
Приведем данную задачу к стандартному виду. Для этого введем новые переменные  Ограничение на управление
Ограничение на управление  задается множеством
задается множеством

Найдем все управления, удовлетворяющие принципу максимума Понтрягина, для чего запишем все условия этого принципа применительно к данной задаче.
Матрица  для системы имеет вид
для системы имеет вид 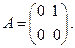 Следовательно,
Следовательно,  и сопряженная система уравнений принимает вид
и сопряженная система уравнений принимает вид

Опорные функции множеств  и
и  вычисляются непосредственно:
вычисляются непосредственно:

Из условия максимума получаем равенство
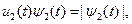
следовательно, имеем

Из условия трансверсальности на множестве  получаем равенство
получаем равенство
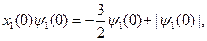
следовательно,

И, наконец, из условия трансверсальности на множестве  получаем равенство
получаем равенство
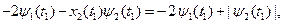
откуда

Рассмотрим решение сопряженной системы с начальным условием  Это решение имеет вид
Это решение имеет вид
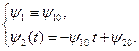
Из условия максимума следует, что управление  удовлетворяющее принципу максимума, зависит от знака функции
удовлетворяющее принципу максимума, зависит от знака функции 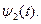 Для тех моментов времени
Для тех моментов времени  для которых
для которых  управление имеет вид
управление имеет вид  Для тех моментов
Для тех моментов  для которых
для которых  управление имеет вид
управление имеет вид 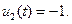 Если в какой – то момент времени
Если в какой – то момент времени  функция
функция  обращается в нуль, то в этот момент времени управление
обращается в нуль, то в этот момент времени управление  из условия максимума не определяется. Оно может принимать произвольное значение
из условия максимума не определяется. Оно может принимать произвольное значение 
Функция  линейно зависит от времени
линейно зависит от времени  и не может тождественно обращаться в нуль, поскольку
и не может тождественно обращаться в нуль, поскольку  Таким образом, функция
Таким образом, функция  может обращаться в нуль не более чем в одной точке. Следовательно, управление
может обращаться в нуль не более чем в одной точке. Следовательно, управление  удовлетворяющее условию максимума, является кусочно постоянным, принимающим лишь два значения -1 и 1, причем оно может менять свое значение не более одного раза именно в тот момент времени
удовлетворяющее условию максимума, является кусочно постоянным, принимающим лишь два значения -1 и 1, причем оно может менять свое значение не более одного раза именно в тот момент времени  когда
когда 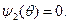 Произвол в выборе управления
Произвол в выборе управления  в одной точке
в одной точке 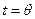 никак не сказывается на решении
никак не сказывается на решении  системы уравнений.
системы уравнений.
Выясним, по какой траектории в фазовой плоскости 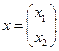 будет двигаться точка
будет двигаться точка  в случае, когда
в случае, когда  В силу системы имеем соотношения
В силу системы имеем соотношения

Исключая время  получаем:
получаем:

то есть

где  постоянная, определяемая начальной точкой траектории. Такие фазовые кривые изображены на рис.3. Они представляют собой семейство парабол, направление движения по которым указано стрелками. Такое направление объясняется тем, что
постоянная, определяемая начальной точкой траектории. Такие фазовые кривые изображены на рис.3. Они представляют собой семейство парабол, направление движения по которым указано стрелками. Такое направление объясняется тем, что  то есть координата
то есть координата  возрастает с течением времени.
возрастает с течением времени.



Рис.3
Аналогично для случая, когда  имеем:
имеем:
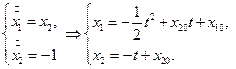
Исключая  получаем:
получаем:

Фазовые траектории для данного случая изображены на рис.4.
Таким образом, в моменты времени  когда
когда  движение фазовой точки
движение фазовой точки  происходит по траекториям, изображенным на рис.3, а в моменты времени
происходит по траекториям, изображенным на рис.3, а в моменты времени  когда
когда  по траекториям, изображенным на рис.4.
по траекториям, изображенным на рис.4.



Рис.4
Построим теперь все управления и траектории, удовлетворяющие принципу максимума Понтрягина. Для этого исследуем поведение линейной функции  Будем выбирать всевозможные начальные значения
Будем выбирать всевозможные начальные значения  Рассмотрим три случая:
Рассмотрим три случая:
I. Если 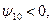 то из условия трансверсальности на множестве
то из условия трансверсальности на множестве  следует, что начальная точка траектории имеет вид
следует, что начальная точка траектории имеет вид  Функция
Функция  в этом случае может быть положительной при всех
в этом случае может быть положительной при всех  (если
(если 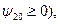 либо до некоторого момента времени
либо до некоторого момента времени  быть отрицательной, а затем стать положительной (если
быть отрицательной, а затем стать положительной (если  (рис.5).
(рис.5).





Рис.5
Следовательно, согласно условию максимума управление  будет иметь вид
будет иметь вид 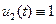 или в некоторый момент времени
или в некоторый момент времени  переключается с -1 на 1. В обоих случаях фазовая траектория
переключается с -1 на 1. В обоих случаях фазовая траектория  выходящая из точки
выходящая из точки 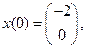 никогда не достигнет множества
никогда не достигнет множества  (рис.6).
(рис.6).












Рис.6
II. Если 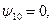 то из соотношения следует, что начальная точка
то из соотношения следует, что начальная точка  может принимать произвольное значение из множества
может принимать произвольное значение из множества  В этом случае
В этом случае  поскольку
поскольку 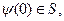 а функция
а функция  либо отрицательна при всех
либо отрицательна при всех  если
если  либо положительна при всех
либо положительна при всех 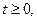 если
если  (рис.7). В силу условия это означает, что управление
(рис.7). В силу условия это означает, что управление  постоянно при всех
постоянно при всех  и равно -1, если
и равно -1, если  или 1, если
или 1, если 



Рис.7
Все траектории с такими постоянными управлениями изображены на рис.8 и ни одна из них не достигает множества 





Рис.8
III. Если  то из условия трансверсальности на множестве
то из условия трансверсальности на множестве  следует, что начальная точка траектории имеет вид
следует, что начальная точка траектории имеет вид  Функция
Функция  в этом случае может быть отрицательной при всех
в этом случае может быть отрицательной при всех  (если
(если  либо до некоторого момента времени
либо до некоторого момента времени  быть положительной, а затем стать отрицательной (если
быть положительной, а затем стать отрицательной (если  (рис.9). При этом момент
(рис.9). При этом момент  может быть сделан произвольным, так как он определяется из условия
может быть сделан произвольным, так как он определяется из условия 





Рис.9
Следовательно, согласно условию максимума управление  будет иметь вид
будет иметь вид  или в некоторый момент времени
или в некоторый момент времени  переключается с 1 на -1. В первом случае фазовая траектория
переключается с 1 на -1. В первом случае фазовая траектория  выходящая из точки
выходящая из точки 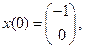 никогда не достигнет множества
никогда не достигнет множества  (рис.10).
(рис.10).





Рис.10
Если управление  вначале равно 1, а затем -1, то при некоторых
вначале равно 1, а затем -1, то при некоторых  траектории такого вида достигнут множества
траектории такого вида достигнут множества  (рис.11). Из рисунка видно, что таких траекторий бесконечно много и в каждую точку множества
(рис.11). Из рисунка видно, что таких траекторий бесконечно много и в каждую точку множества  попадает одна траектория данного вида. Проверим условие трансверсальности на множестве
попадает одна траектория данного вида. Проверим условие трансверсальности на множестве  . Поскольку для всех траекторий данного вида
. Поскольку для всех траекторий данного вида  из соотношения следует, что конечная точка траектории
из соотношения следует, что конечная точка траектории  определяется условием
определяется условием  Этому конечному условию удовлетворяет лишь одна траектория данного типа. На рис. 11 она изображена жирной линией.
Этому конечному условию удовлетворяет лишь одна траектория данного типа. На рис. 11 она изображена жирной линией.





Рис.11
Найдем эту единственную траекторию, удовлетворяющую принципу максимума. Точка  лежит на пересечении параболы
лежит на пересечении параболы  проходящей через точку
проходящей через точку  и параболы
и параболы  проходящей через точку
проходящей через точку  Найдем ее, исходя из этого условия. Первая парабола задается уравнением
Найдем ее, исходя из этого условия. Первая парабола задается уравнением  а вторая:
а вторая:  Точка их пересечения находится из системы
Точка их пересечения находится из системы

Движение начинается из точки  с управлением
с управлением  Найдем траекторию
Найдем траекторию  из системы с учетом начального условия:
из системы с учетом начального условия:

По этой траектории точка будет двигаться до момента времени  который определяется из условия попадания траектории
который определяется из условия попадания траектории  в точку
в точку  Имеем
Имеем  откуда,
откуда,  Начиная с этого момента времени управление
Начиная с этого момента времени управление  равно -1. Дальнейшую траекторию найдем из системы с учетом начального условия
равно -1. Дальнейшую траекторию найдем из системы с учетом начального условия 
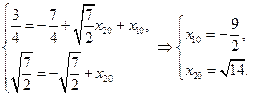
Таким образом, соответствующее решение имеет вид

Момент времени 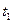 определяется из условия попадания траектории в конечную точку
определяется из условия попадания траектории в конечную точку  Получаем
Получаем

Итак, мы установили, что единственное управление 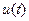 удовлетворяет принципу максимума Понтрягина и переводит объект из множества
удовлетворяет принципу максимума Понтрягина и переводит объект из множества  на множество
на множество  на отрезке времени
на отрезке времени 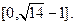 По теореме существования оптимального управления в данной задаче оптимальное управление существует. По теореме о необходимых условиях оптимальности это управление должно удовлетворять принципу максимума. А так как мы нашли единственное управление
По теореме существования оптимального управления в данной задаче оптимальное управление существует. По теореме о необходимых условиях оптимальности это управление должно удовлетворять принципу максимума. А так как мы нашли единственное управление 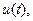 удовлетворяющее принципу максимума, то, следовательно, это управление
удовлетворяющее принципу максимума, то, следовательно, это управление 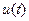 оптимально.
оптимально.
Ответ:  оптимальное управление,
оптимальное управление,

 соответствующая ему траектория,
соответствующая ему траектория,  наименьшее время перехода из множества
наименьшее время перехода из множества  на множество
на множество 
Пример 15. Решить задачу быстродействия


Решение. Не ограничивая общности, будем считать, что  Приведем данную задачу к стандартному виду. Для этого введем новые переменные
Приведем данную задачу к стандартному виду. Для этого введем новые переменные  Ограничение на управление
Ограничение на управление  задается множеством
задается множеством
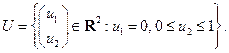
Найдем все управления, удовлетворяющие принципу максимума Понтрягина, для чего запишем все условия этого принципа применительно к данной задаче.





Рис.12
Матрица  для системы имеет вид
для системы имеет вид 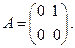 Следовательно,
Следовательно,  и сопряженная система уравнений принимает вид
и сопряженная система уравнений принимает вид

Из условия максимума получаем равенство

следовательно, имеем

Из условия трансверсальности на множестве  получаем, что вектор
получаем, что вектор  является опорным вектором к множеству
является опорным вектором к множеству  в точке
в точке  поэтому
поэтому

И, наконец, из условия трансверсальности на множестве  получаем, что вектор
получаем, что вектор  является опорным вектором к множеству
является опорным вектором к множеству  в точке
в точке  поэтому
поэтому
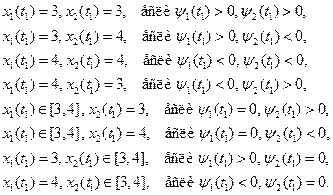
Рассмотрим решение сопряженной системы с начальным условием  Это решение имеет вид
Это решение имеет вид

Из условия максимума следует, что управление  удовлетворяющее принципу максимума, зависит от знака функции
удовлетворяющее принципу максимума, зависит от знака функции 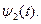 Для тех моментов времени
Для тех моментов времени  для которых
для которых  управление имеет вид
управление имеет вид  Для тех моментов
Для тех моментов  для которых
для которых  управление имеет вид
управление имеет вид 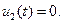 Если в какой – то момент времени
Если в какой – то момент времени  функция
функция  обращается в нуль, то в этот момент времени управление
обращается в нуль, то в этот момент времени управление  из условия максимума не определяется. Оно может принимать произвольное значение
из условия максимума не определяется. Оно может принимать произвольное значение 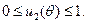
Функция  линейно зависит от времени
линейно зависит от времени  и не может тождественно обращаться в нуль, поскольку
и не может тождественно обращаться в нуль, поскольку  Таким образом, функция
Таким образом, функция  может обращаться в нуль не более чем в одной точке. Следовательно, управление
может обращаться в нуль не более чем в одной точке. Следовательно, управление  удовлетворяющее условию максимума, является кусочно постоянным, принимающим лишь два значения 0 и 1, причем оно может менять свое значение не более одного раза именно в тот момент времени
удовлетворяющее условию максимума, является кусочно постоянным, принимающим лишь два значения 0 и 1, причем оно может менять свое значение не более одного раза именно в тот момент времени  когда
когда 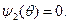 Произвол в выборе управления
Произвол в выборе управления  в одной точке
в одной точке 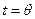 никак не сказывается на решении
никак не сказывается на решении  системы уравнений. При этом момент
системы уравнений. При этом момент  определяется из условия
определяется из условия  то есть
то есть  Следовательно, переключение управления возможно лишь в том случае, когда
Следовательно, переключение управления возможно лишь в том случае, когда  и
и  одного знака.
одного знака.
Выясним, по какой траектории в фазовой плоскости 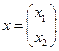 будет двигаться точка
будет двигаться точка  в случае, когда
в случае, когда  В силу системы имеем соотношения
В силу системы имеем соотношения

Исключая время  получаем:
получаем:

то есть

где  постоянная, определяемая начальной точкой траектории. Такие фазовые кривые изображены на рис.2.
постоянная, определяемая начальной точкой траектории. Такие фазовые кривые изображены на рис.2.
Аналогично для случая, когда  имеем:
имеем:

Фазовые траектории для данного случая изображены на рис.13.
Построим теперь все управления и траектории, удовлетворяющие принципу максимума Понтрягина. Для этого исследуем поведение линейной функции  Будем выбирать всевозможные начальные значения
Будем выбирать всевозможные начальные значения  Рассмотрим следующие случаи:
Рассмотрим следующие случаи:





Рис.13
I. Если  то из условия трансверсальности на множестве
то из условия трансверсальности на множестве  следует, что начальная точка траектории имеет вид
следует, что начальная точка траектории имеет вид  Функция
Функция  в этом случае может быть положительной при всех
в этом случае может быть положительной при всех 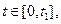 либо, начиная с некоторого момента времени
либо, начиная с некоторого момента времени 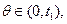 стать отрицательной. Следовательно, согласно условию максимума управление
стать отрицательной. Следовательно, согласно условию максимума управление  будет иметь вид
будет иметь вид 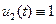 или в некоторый момент времени
или в некоторый момент времени  переключается с 1 на 0. В первом случае фазовая траектория
переключается с 1 на 0. В первом случае фазовая траектория  выходящая из точки
выходящая из точки 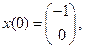 достигнет множества
достигнет множества  в точке
в точке  (рис.14) и условие трансверсальности на множестве
(рис.14) и условие трансверсальности на множестве  не выполнено: так как
не выполнено: так как 
 то в силу
то в силу  должна иметь вид
должна иметь вид  .
.





Рис.14
Во втором случае, если переключение управления  с 1 на 0 происходит до момента попадания траектории на множество
с 1 на 0 происходит до момента попадания траектории на множество  движение продолжается по прямым
движение продолжается по прямым 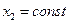 и точка никогда не попадет на конечное множество
и точка никогда не попадет на конечное множество  (рис.15). Если же переключение происходит в момент попадания траектории в точку
(рис.15). Если же переключение происходит в момент попадания траектории в точку  то
то 
 и условие трансверсальности не выполнено.
и условие трансверсальности не выполнено.





Рис.15
II. Если  то в силу начальная точка траектории имеет вид
то в силу начальная точка траектории имеет вид  Функция
Функция  в этом случае является отрицательной при всех
в этом случае является отрицательной при всех  Следовательно, согласно условию максимума управление
Следовательно, согласно условию максимума управление  и фазовая траектория
и фазовая траектория  никогда не достигнет множества
никогда не достигнет множества  (рис.16).
(рис.16).





Рис.16
III. Если  то в силу условия трансверсальности на множестве
то в силу условия трансверсальности на множестве  начальная точка траектории имеет вид
начальная точка траектории имеет вид  Функция
Функция  в этом случае может быть отрицательной при всех
в этом случае может быть отрицательной при всех  либо, начиная с некоторого момента времени
либо, начиная с некоторого момента времени  стать положительной. Следовательно, согласно условию максимума управление
стать положительной. Следовательно, согласно условию максимума управление  или в некоторый момент времени
или в некоторый момент времени  управление переключается с 0 на 1. В первом случае фазовая траектория
управление переключается с 0 на 1. В первом случае фазовая траектория  выходящая из точки
выходящая из точки  никогда не достигнет множества
никогда не достигнет множества  (рис.17).
(рис.17).





Рис.17
Во втором случае существует бесконечно много траекторий, достигающих множества  в точках
в точках  (рис.18). Проверим для каких из этих траекторий выполняется условие трансверсальности на множестве
(рис.18). Проверим для каких из этих траекторий выполняется условие трансверсальности на множестве  В силу того, что
В силу того, что 
 из следует, что
из следует, что  должна иметь вид
должна иметь вид  Этому конечному условию не удовлетворяет ни одна из указанных траекторий.
Этому конечному условию не удовлетворяет ни одна из указанных траекторий.





Рис.18
IV. Если  то в силу условия трансверсальности на множестве
то в силу условия трансверсальности на множестве  начальная точка траектории имеет вид
начальная точка траектории имеет вид  Функция
Функция  в этом случае положительна при всех
в этом случае положительна при всех  Следовательно, согласно условию максимума управление
Следовательно, согласно условию максимума управление 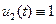 и фазовая траектория
и фазовая траектория  выходящая из точки
выходящая из точки  достигнет множества
достигнет множества  в точке
в точке 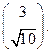 (рис.19). Проверим выполнение условия трансверсальности на множестве
(рис.19). Проверим выполнение условия трансверсальности на множестве  для данной траектории: так как
для данной траектории: так как 
 то в силу
то в силу  Таким образом, условие трансверсальности для найденной траектории не выполнено.
Таким образом, условие трансверсальности для найденной траектории не выполнено.






Рис.19
V. Если 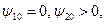 то в силу начальная точка траектории не определяется однозначно и является любой точкой множества
то в силу начальная точка траектории не определяется однозначно и является любой точкой множества  Функция
Функция  в этом случае тождественно равна
в этом случае тождественно равна  Согласно условию максимума
Согласно условию максимума 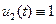 и существует бесконечно много траекторий
и существует бесконечно много траекторий  достигающих
достигающих  в точках множества
в точках множества

Проверим для каких из этих траекторий выполняется условие трансверсальности на множестве  В силу того, что
В силу того, что 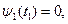
 из имеем
из имеем  Таким образом, принципу максимума удовлетворяют траектории, достигающие множества
Таким образом, принципу максимума удовлетворяют траектории, достигающие множества  в точках множества
в точках множества  то есть траектории, начальные точки которых принадлежат множеству
то есть траектории, начальные точки которых принадлежат множеству  На рис.20 они изображены жирными линиями.
На рис.20 они изображены жирными линиями.





Рис.20
Найдем время перехода из множества  на множество
на множество  по данным траекториям. Семейство парабол описывается уравнениями
по данным траекториям. Семейство парабол описывается уравнениями

Так как в конечный момент времени 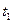 для всех траекторий семейства
для всех траекторий семейства  то из второго уравнения получаем, что
то из второго уравнения получаем, что 
VI. Если  то в силу начальная точка траектории не определяется однозначно:
то в силу начальная точка траектории не определяется однозначно:  Функция
Функция  в этом случае тождественно равна
в этом случае тождественно равна  и согласно условию максимума
и согласно условию максимума  Фазовые траектории в данном случае не достигают множества
Фазовые траектории в данном случае не достигают множества  (рис.21).
(рис.21).





Рис.21
VII. Если  то начальная точка траектории принадлежит множеству
то начальная точка траектории принадлежит множеству 
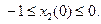 Функция
Функция  в этом случае отрицательна при всех
в этом случае отрицательна при всех  и согласно условию максимума
и согласно условию максимума  Фазовые траектории в данном случае не достигают множества
Фазовые траектории в данном случае не достигают множества  (рис.22).
(рис.22).




Рис.22
VIII. Если  то начальная точка траектории принадлежит множеству
то начальная точка траектории принадлежит множеству 
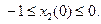 Функция
Функция  в этом случае положительна при всех
в этом случае положительна при всех  и согласно условию максимума
и согласно условию максимума  Таким образом, существует бесконечно много траекторий, достигающих множества
Таким образом, существует бесконечно много траекторий, достигающих множества  (рис.23) в точках множества
(рис.23) в точках множества  Проверим выполнение для данных траекторий условия трансверсальности на множестве
Проверим выполнение для данных траекторий условия трансверсальности на множестве  Так как
Так как 
 то из имеем
то из имеем  Этому конечному условию не удовлетворяет ни одна из найденных траекторий.
Этому конечному условию не удовлетворяет ни одна из найденных траекторий.





Рис.23
Ответ:  оптимальное управление,
оптимальное управление, 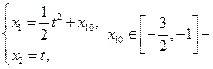 соответствующие ему траектории,
соответствующие ему траектории,  – наименьшее время перехода из множества
– наименьшее время перехода из множества  на множество
на множество 
Пример 16. Решить задачу быстродействия

Решение. Приведем данную задачу к стандартному виду. Для этого введем новые переменные 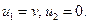 Ограничение на управление
Ограничение на управление  задается множеством
задается множеством

Дата добавления: 2015-09-05; просмотров: 185 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ИНТЕГРАЛ АУМАННА | | | КОНТРОЛЬНАЯ РАБОТА № 1 |