Лінійні задачі керування

А. В. Арсірій, О. Д. Кічмаренко, Н. В. Скрипник

Многозначний аналіз та

лінійні задачі керування

Методичні вказівки та варіанти контрольних робіт

для студентів 3 - 6 курсів

Одеса

«Астропринт»

Методичні вказівки та варіанти контрольних робіт до спецкурсу “Многозначний аналіз та лінійні задачі керування ” для студентів 3 - 6 курсів факультету прикладної математики і комп’ютерних мереж.

Рецензенти: А. В. Плотніков, д. ф. - м. н., професор,

О. А. Тінгаєв, к. ф. - м. н., доцент

Рекомендовано до друку Вченою радою ІМЕМ ОНУ ім. І. І. Мечникова.

Протокол № 2 від “ 14” листопада 2006 р.

© А. В. Арсірій, О. Д. Кічмаренко,

Н. В. Скрипник, 2008

СОДЕРЖАНИЕ

Литература. 4

Пространства и 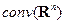............... 5

Опорная функция и ее основные свойства. 14

Многозначные отображения. Интеграл Ауманна. 20

Линейная задача быстродействия. Принцип максимума Понтрягина. 26

Контрольная работа № 1. 51

Контрольная работа № 2. 62

Контрольная работа № 3. 70

Контрольная работа № 4. 71

ЛИТЕРАТУРА

1. Благодатских В.И. Введение в оптимальное управление. – М.:Высш.шк., 2001. – 239 с.

2. Благодатских В.И. Линейная теория оптимального управления. – М.:Изд-во МГУ, 1978. – 94 с.

3. Благодатских В.И. Теория дифференциальных включений. – М.:Изд-во МГУ, 1979.

4. Борисович Ю.Г., Гельман Б.Д., Мышкис А.Д., Обуховский В.В. Введение в теорию многозначных отображений и дифференциальных включений. – М.: КомКнига, 2005. – 216 с.

5. Половинкин Е.С. Теория многозначных отображений. М.: Изд-во МФТИ, 1983.

6. Филатов О.П. Лекции по многозначному анализу и дифференциальным включениям.- Самара: Изд-во “Самарский университет”, 2000. – 116 с.

7. Филиппов А.Ф. Дифференциальные уравнения с разрывной правой частью. – М.: Наука, 1985. – 224 с.

8. Aumann R.J. Integrals of set - valued functions // J. Math. Anal. Appl. – 1965. – Vol.12, № 1. – P.1 – 12.

ПРОСТРАНСТВА И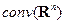

Пусть - - мерное евклидово век­торное пространство с элементами Пространство является линей­ным пространством с обычными операциями сложения векто­ров, умножения вектора на число и скалярным произведением а также нормированным пространством с нормой .

Рассмотрим пространство , состоящее из всех непус­тых компактных подмножеств пространства

Определение 1. Алгебраической сум­мой или просто суммой двух множеств и из пространства называется множество

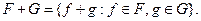
Сумма + двух множеств и из пространства является также Элементом пространства 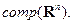Кроме того, если множества , выпуклы, то их алгебраическая сум­ма + также будет выпуклым множеством.

Если множество состоит из единственной точки, то есть 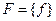, то множество получается параллельным сдвигом множества на вектор .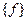

Пусть шар радиуса с центром в точке то есть

Тогда

то есть при сложении двух шаров их радиусы суммируются и векторы, задающее центры шаров, также суммируется.

Из этой формулы при мы получаем, что

Операция алгебраической суммы для любых множеств 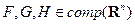удовлетворяет следующим свойствам:

1) коммутативности

2) ассоциативности

3) существует нулевой элемент :

Следует отметить, что если множество состоит более чем из одной точки, то у такого множества нет обратного элемента относительно введенной операции суммы множеств, то есть не существует такое множеств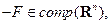о что Если же 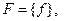то

Пример 1. Найти сумму множеств и заданных аналитически или изображенных на рисунке:

1) Пусть Тогда по определению суммы множеств

2) Пусть 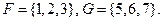Тогда по определению суммы множеств

3) Пусть множества и изображены на рисунке:

Так как множество одноточечное, то множество получается из множества параллельным сдвигом на 5 единиц вправо:

4) Пусть множества и изображены на рисунке:

Для любых элементов справедливы неравенства 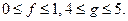Тогда сумма 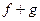удовлетворяет неравенству Таким образом,

Кроме того, для любого элемента существуют элементы 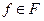и такие, что например при и при 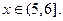Следовательно, Окончательно множество имеет вид:

5) Пусть множества и изображены на рисунке:

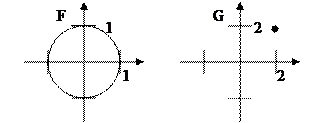
Так как множество одноточечное, то множество получается из множества параллельным переносом на вектор :

6) Пусть множества и изображены на рисунке:

Для любой точки множество получается из множества параллельным сдвигом на вектор то есть представляет собой окружность единичного радиуса с центром в точке Когда элемент “пробегает” множество окружность “движется” параллельно оси в результате образуя выпуклое множество, изображенное на рисунке:

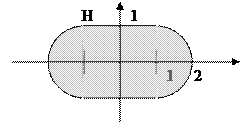
7) Пусть множества и изображены на рисунке:

Аналогично предыдущему примеру получаем:

8) Пусть множества и изображены на рисунке:

Для любой точки множество получается из множества параллельным сдвигом на вектор то есть представляет собой окружность единичного радиуса с центром в точке Когда элемент “пробегает” множество центр окружности движется по единичной окружности в результате получаем выпуклое множество S₂(0), изображенное на рисунке:

9) Пусть множества и изображены на рисунке:

Аналогично предыдущему примеру получаем:

10) Пусть множества и изображены на рисунке:

Тогда аналогично предыдущему их сумма имеет вид:

11) Пусть множества и изображены на рисунке:

Тогда аналогично предыдущему их сумма имеет вид:

Определение 2. Произведением мно­жества 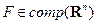на число называется множество

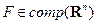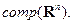Произведение на произвольное число является элементом пространства Кроме того, если множество выпуклое, то и множество также выпуклое.

При умножении шара радиуса с центром в a на число радиус шара умножается на а центр – на то есть

Таким образом, учитывая формулу, имеем

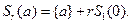
Непосредственно проверяется, что для любых чисел 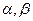и любых двух множеств выполняются следующие свойства:

1)

2)

3)

Пространство не является линейным пространством с введенными операциями алгебраической суммы двух множеств и умножения множества не число хотя бы потому, что не у каждого элемента 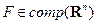есть обратный элемент Кроме того, не всегда выполняется необходимый для линейности закон дистрибутивности, то есть не всегда выполняется равенство:

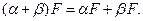
Вместо равенства в формуле справедливо лишь одностороннее включение

Оказывается, что если и множество выпукло, то формула в этом случае справедлива.

Пример 2. Найти произведение множества на скаляр

1) Пусть F ={1,5}, l=2. Тогда

2) Пусть 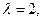множество F изображено на рисунке:

Тогда для любого элемента 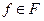справедливо неравенство а значит для любого элемента справедливо неравенство то есть Кроме того, для любого элемента найдется элемент такой, что то есть Окончательно получаем, что множество имеет вид:

3) Пусть 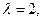множество F – единичная сфера в пространстве

Тогда в силу определения 2 множество G – сфера радиуса 2 с центром в начале координат:

4) Пусть F – единичный шар в пространстве

Тогда в силу множество G – шар радиуса 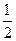с центром в начале координат:

5) Пусть F – единичный квадрат,

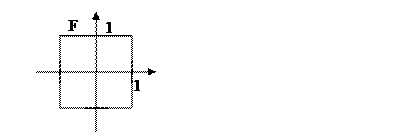
Тогда в силу определения 2 любому элементу 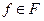соответствует элемент то есть множество симметрично множеству относительно начала координат. В данном примере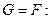

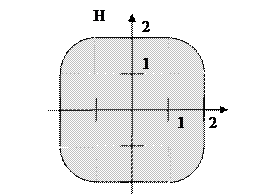
6) Пусть множество F изображено на рисунке:

Аналогично предыдущему примеру множество симметрично множеству относительно начала координат:

Рассмотрим подпространство 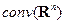пространства , состоящее из всех непустых выпуклых компактных под­множеств пространства Приведенные выше свойства опера­ций алгебраической суммы множеств и умножения множества на число показывают, что если рассматривать умножение вы­пуклых множеств только на неотрицательные числа, то для пространства 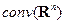справедливы все аксиомы линейнос­ти, кроме аксиомы существования обратного элемента.

Пусть 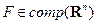и в пространстве задано линейное пре­образование с помощью матрицы (с действительными эле­ментами) размером .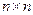

Определение 3. Образом множества при линейном преобразовании, задаваемом матрицей , называется множество

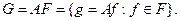
Легко проверить, что образ множества 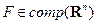при линейном преобразовании также является элементом пространства 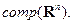Кроме того, если множество выпуклое, то и множество также выпукло.

Дата добавления: 2015-09-05