
Читайте также:
|
Цель раборы: научиться разрабатывать и отлаживать программы для вычисления определенных интегралов численными методами прямоугольников и трацеций
Приближенное значение определенного интеграла вычисляется как сумма площадей N прямоугольников, построенных на интервале интегрирования [ a,b]. Интервал [ a,b] разбивается на N равных частей длиной h = (b- a)/N, на каждой из которых строится прямоугольник с высотой, равной значению функции f(xi) в центре участка с координатой
xi = a +(i-0.5)h, где i=1,2,...,N
Формула прямоугольников для приближенного вычисления значения интеграла будет иметь вид
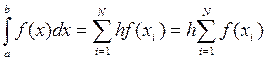 .
.
В методе трапеций весь интервал [ a,b] разбивается на N равных частей длиной h=(b- a)/N, на каждой из которых строится трапеция. Приближенное значение ин- теграла определяется суммой площадей этих трапеций
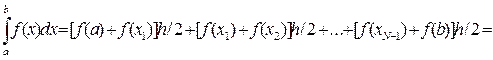
 ,
,
где xi = a +i* h.
Разработать программу для вычисления значения определенного интеграла на интервале [a,b] (a, b подобрать самостоятельно) численными методами прямоугольников и трапеций [8, 9] для следующих вариантов:
1. 
 2.
2. 
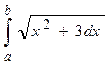 3.
3. 
4.  5.
5.  6.
6. 
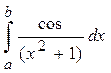
7.  8.
8.  9.
9. 
10.  11.
11. 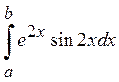 12.
12. 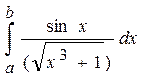
13.  14.
14.  15.
15. 
16. 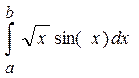 17.
17.  18.
18. 
19.  20.
20. 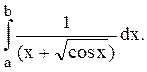
Интервал интегрирования разбить равномерно на N>50 частей.
Дата добавления: 2015-09-05; просмотров: 61 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание (программа_13) | | | Графика |