Читайте также:
|
Для частного случая, когда представляемая числовая последовательность имеет конечную длительность (конечное число ненулевых значений), можно разработать другой вид преобразования Фурье – ДПФ. ДПФ – это последовательность, которая соответствует равноудалённым по частоте отсчётам обычного преобразования Фурье.
Для правильной интерпретации ДПФ конструируется периодическая последовательность, каждый период которой совпадает с последовательностью конечной длины. Тогда дискретный ряд Фурье этой периодической последовательности соответствует ДПФ последовательности этой конечно длины.
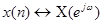ПФ.
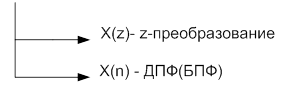
Пример: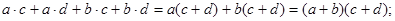 
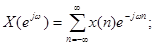
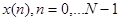- конечная последовательность.
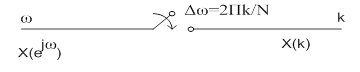
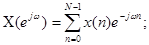
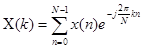- ДПФ, k=0,1…N-1.
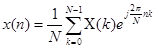-ОПФ, n=0,1…N-1.
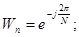
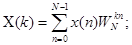
Свойства ДПФ:
1) ДПФ – линейное преобразование. Сумме сигналов отвечает сумма их ДПФ.
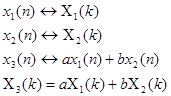
Пусть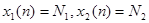 
, тогда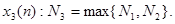 
Пусть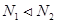 
, тогда 
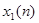дополняется до длительности 
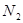нулями и расчет ДПФ ведется по следующим формулам:
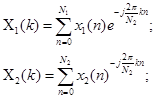
2) Число различных коэффициентов ДПФ, т.е.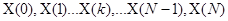 
, равно числу членов числовой последовательности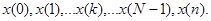 
Всегда важно помнить, что когда речь идет о ДПФ, последовательность x(n) конечной длины, представляются как один период периодической последовательности.
3) Коэффициент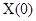 
(постоянная составляющая) является суммой всех отсчетов входной последовательности.
4) Если N четное число, то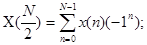 
5) Пусть x(n) – вещественно, тогда коэффициенты ДПФ, номера которых располагаются симметрично относительно N/2, образуют сопряженные пары: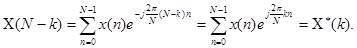 
Поэтому можно считать, что коэффициенты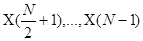 
отвечают отрицательным частотам, они не дают новых сведений
Дата добавления: 2015-09-04; просмотров: 107 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Билет 13. | | | Понятие стационарности и эргодичности случайных процессов. |