Читайте также:
|
Случайные процессы можно классифицировать следующим образом
1.Стационарные.
2.Нестационарные.
Стационарные процессы – стационарны в узком смысле (СУС) и стационарны в широком смысле (СШС).
СУС – процессы, все N-мерные моменты функции которых, а также функция распределения и плотность распределения, не зависит от момента времени, а зависит от их взаимного расположения на оси.
Предъявленные требования очень жесткие, таких процессов мало, класс узок.
СШС – процессы, отвечающие следующим условиям:
1. 
2. 
3. 
Корреляционная функция одной переменной: 
Нестационарные процессы:
Стационарные процессы бывают эргодические и неэргодические.
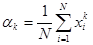-усреднение по ансамблю (поперек).
Если о стационарном процессе можно судить на основании одной реализации достаточной длительности, то он эргодический. Статистическая характеристика такого процесса, найденного по множеству реализаций и по одной реализации с бесконечной длительностью совпадает с вероятностью, стремящейся к 1.
- усреднение по 1 реализации (вдоль).
Если характеристики полученные усреднением поперек и вдоль совпадает, то такой процесс называется эргодическим.
Дата добавления: 2015-09-04; просмотров: 149 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Преобразование Фурье последовательности конечной длительности. Свойства ДПФ | | | Ряд Фурье. |