1. Расчёт КИХ-фильтров с использованием окон.
Пусть 
идеальная требуемая частотная характеристика.
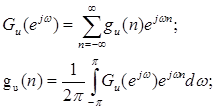
Такой фильтр невозможно реализовать, так как бесконечная импульсная характеристика
Единственным путем для получения физически реализуемой, импульсной характеристики является простое усечение 
, где в качестве 
может быть использована произвольная последовательность конечной длины, например, прямоугольная.
Это преобразование Фурье от окна.
Умножение во временной области соответствует свертке в частотной, т.е. частотная хар-ка фильтра с конечной ИХ будет иметь вид:
После получения сверки получаем размытую версию идеальной ЧХ. Размытая версия получается путем резкого усечения ЧХ.
Явления Гиббса можно уменьшить путем постепенного снижения окна до нуля. Это называется уменьшением высоты боковых лепестков, за счет увеличения ширины основного лепестка, что, в конечном счете, ведет к более широкой переходной полосе.
Приведем графики некоторых окон:
Дата добавления: 2015-09-04; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание требований к ЦФ в частотной области | | | Классификация и модели биомедицинских сигналов |