Классификация и модели биомедицинских сигналов

Сигнал - материальный носитель информации.

Информация – это совокупность сведений, уменьшающих начальную неопределенность состояния материального объекта.

Для того чтобы сделать сигнал объектом теоретического исследования, следует указать способ его математического описания. Т.е. разработать математическую модель исследуемого объекта. В качестве математической модели будем использовать функциональную зависимость.

Каузальным называют сигнал, который имеет начало во времени, т.е. является следствием какой-то причины.

Финитным называют сигнал, локализованный во времени.

Непрерывным называют сигнал, который рассматривается в каждой точке оси времени и задан на несчетном множестве временной оси.

Дискретным называется сигнал, только в фиксированные моменты времени. Значение дискретного сигнала называется отсчетом. Если отсчет представлен числом, то это цифровой сигнал.

Детерминированный сигнал описывается точными математическими зависимостями, позволяющими указать значение сигнала в любой момент времени.

Периодический сигнал описывается функцией вида: x(t)=x(t+nt), n=±1, ±2.

T – период. Т=[c].

Величина обратная периоду называется частотой.

;

;

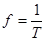Частота f является фундаментальной или основной частотой.

- круговая или угловая частота.

f показывает число периодов за 1 секунду. ω- показывает число периодов за 2π.

гармонический сигнал:

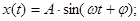
А-амплитуда;

ω- частота;

φ- начальная фаза;

А, ω, φ=const.

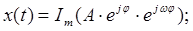
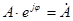– комплексная амплитуда

Представление сигнала в координатах амплитуда-частота и есть спектр:

А̀= = ;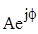

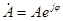-показательная форма.

- вещественная часть.

Гармонический сигнал является собственной функцией линейных систем.

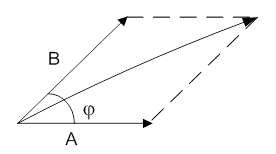
Полигармонические сигналы – это сигналы, которые могут быть представлены в виде суммы двух и более гармонических сигналов, частоты которых находятся в рациональном отношении.

Радиальное число:

Можно подобрать такую, что:

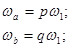
ω 1- частота первой гармоники, основного тона.

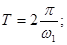
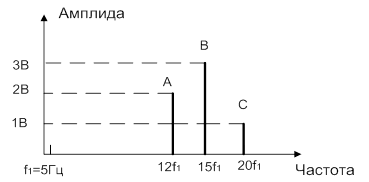
Множество амплитуд {Ak} полигармонического сигнала называется спектром амплитуд.

{φК}- спектр фаз;

{А̀к} – комплексный спектр;

В общем случае полигармонические сигналы описываются так:

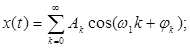
Почти периодические сигналы описываются функцией вида:

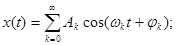
Функции вида, где среди ωк найдутся такие ωm и ωn, отношение которых иррациональное число:

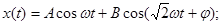
Сигнал называется почти периодическим, если для любого έ >0 можно найти такое число l>0, что любой интервал оси времени t, длиной l, будет содержать хотя бы одно значение τ, для которого для всех t выполнялось неравенство:

Дискретный или линейчатый спектр:

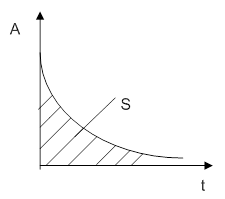
Переходные сигналы – все те непериодические сигналы, которые не являются почти периодическими. Переходные сигналы имеют не дискретный, а непрерывный (сплошной) спектр.

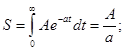
Дата добавления: 2015-09-04