
|
Читайте также: |
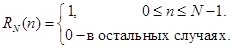
Изобразим на рисунке следующие 4 последовательности:

Сравнение показывает, что x1(n) – не соответствует линейному сдвигу x(n).
Для трактовки такого сдвига представим, что последовательность конечной длины x(n) расположена на поверхности цилиндра в N точках. При движении по поверхности цилиндра наблюдаемая последовательность будет периодической последовательностью x̃(n). При этом линейный сдвиг последовательности x̃(n) соответствует вращению цилиндра. Такой сдвиг называется круговым.
Дата добавления: 2015-09-04; просмотров: 50 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Спектры непериодических сигналов. Интеграл Фурье. | | | Билет 20. |