


2. Вычисление линейной свёртки с помощью ДПФ
Вычислить линейную свертку двух последовательностей можно следующим способом:
1. Дополнить нулями – будем рассматривать последовательность с длительностью 2N, если 2N точечную круговую свёртку этих последовательностей, то получим результат, идентичный линейной свёртке этих последовательностей
2. Вычислить ДПФ 2N точечных последовательностей.
3. Перемножить эти ДПФ.
4. Вычислить ОДПФ (нужно считать БПФ, тогда количество операций станет меньше).
Видно, что умножение ДПФ соответствует круговой свёртке, а не линейной, поэтому необходимо, чтобы круговая свёртка давала результат линейной последовательности.
Рассмотрим N точечных последовательностей:
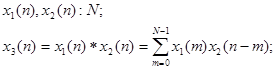
Непосредственно проверяется, что x3(n) имеет длину 2N-1.
Чтобы получить x3(n) при помощи ДПФ, оно должно вычисляться на основе 2N-1 точек, т.е.:
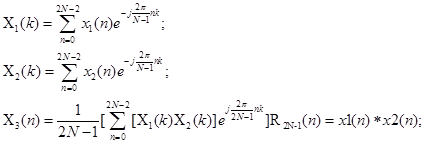
В общем случае, если x1(n) имеет длинуN1, а x2(n) – N2, то их свертка будет иметь длину N1+ N2-1, поэтому ДПФ следует вычислять на основе 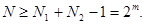
Существуют методы, позволяющие с помощью ДПФ вычислять свертку последовательности конечной длины с последовательностью бесконечной длины.
Например, при фильтрации кардиосигнала, речевого сигнала. Бесконечный сигнал разбивается на секции конечной длительности. Каждая секция свертывается затем с импульсной характеристикой конечной длительности, и отфильтрованные секции собираются вместе подходящим образом.
Дата добавления: 2015-09-04; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Круговой сдвиг последовательности. | | | Представление цифровых сигналов и систем в частотной области. Частотная характеристика |