Выборочный метод в статистическом анализе

Математическая статистика – раздел математики, косвенно устанавливает закономерности случайных явлений или процессов на основании регистрации, систематизации обработки наблюдений или измерений.

Статистика связана с описанием больших совокупностей объектов, но множество чисел, малодоступность, дороговизна изучения этой совокупности, приводит к необходимости изучения какой-то части этой совокупности. Эта часть называется выборкой или выборочной совокупности, а вся совокупность называется генеральной совокупностью (ГС).

Задача суждения о большом по малому, о бесконечном по конечному, решается с помощью выборочного метода.

- генеральная совокупность. Извлекаем выборку из ГС: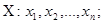

Единственным способ сделать выборку репрезентативной - нужно сделать случайный выбор.

Требования к выборке:

1. Выбор должен быть случайный, отсюда все выборки носят случайный характер.

2. Поскольку мы обеспечиваем возможность всем элементам из ГС попасть в выборку, то на месте 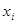- элемента выборки может оказаться любой элемент ГС . Каждый элемент выборки есть случайный вектор.

3. На месте 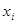может оказаться любой элемент ГС. Совокупность возможных значений 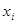есть сама ГС, т.е. каждый элемент выборки 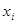имеет то же самое распределение, что и .

ГС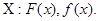

Пусть ГС имеет нормальное распределение.

Так как элементы выборки статистически независимы, совместная плотность распределения выборки определяется, как:

Тоже самое для функции распределения.

Совместная функция распределения выборки называется функция правдоподобия и обозначается как L.

Выборку можно рассматривать двояко:

1. - случайные величины.

2. 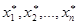- конкретные числа.

Подставим в функцию правдоподобия числа, полученные в результате эксперимента.

Эта функция правдоподобия характеризует зависимость вероятности появления конкретной выборки от параметров распределения θ. Если θ – известно, то функция правдоподобия определяет вероятность появления именно этой выборки.

Дата добавления: 2015-09-04