Оценка премии европейского опциона. Премию европейских опционов колл и пут для купонных обли-

Премию европейских опционов колл и пут для купонных обли-

гации можно определить с помощью формул Блека-Сколеса

ce = BN (d 1)- Xe

- rT

N (d 2); d 2 =

ln(B

X)+(r +σ 2 2) T

σ T

pe = Xe

- rT

N (- d 2)-β N (- d 1)

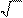d 2 = d 1 -σ T

где — β текущая цена облигации.

Если в течение действия опционного контракта по облигации выплачиваются купоны, то цену облигации В необходимо умень- шить на приведенную стоимость купонов. Стандартное отклоне- ние цены облигации рассчитывается, исключая приведенную стоимость купонных платежей. Как известно, цена облигации мо- жет значительно отличаться от ее номинала, когда до погашения бумаги остается много времени. По мере приближения времени выкупа облигации цена ее приближается к нарицательной стоимо- сти. В связи с этим меняется стандартное отклонение ее цены. Поэтому вышеприведенные формулы следует использовать в слу- чаях, когда срок опционного контракта существенно меньше вре- мени, остающегося до погашения облигации.

В качестве цены исполнения может быть принята а) полная цена облигации, то есть цена с учетом той части купонного платежа, которую покупатель должен уплатить продавцу, когда исполнение контракта приходится на какой-либо момент в течение купонного периода; или б) котировочная цена, то есть чистая цена облигации. Она не включает упомянутую часть купонного платежа. В этом случае к котировочной цене необходимо прибавить сумму купона, которая причитается продавцу, и полученный результат подста- вить в формулу в качестве значения X.

Европейские опционы на облигации с нулевым купоном также

определяются по вышеприведенным формулам. Американский опцион колл на облигацию с нулевым купоном не выгодно испол- нять раньше срока истечения контракта, поэтому его премия будет равна премии европейского опциона.

Дата добавления: 2015-08-27