Стандартное отклонение

Важным элементом, который присутствует в моделях оценки премии опционов, является стандартное отклонение. Поэтому ос- тановимся на этом вопросе несколько подробнее.

Вкладчика, инвестирующего свои средства в опционные контр- акты, интересует не только направление движения рынка, но и скорость этого движения, поскольку от нее зависит вероятность

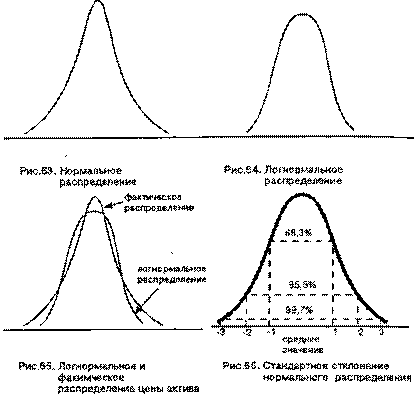
того, что стоимость актива перешагнет за цену исполнения опци- она. Показателем такой скорости выступает стандартное отклоне- ние цены актива или, как его еще именуют, волатильность. Стандартное отклонение говорит о вероятности цены принять то или иное значение. Оно задает Меру рассеянности цены актива. Большое значение стандартного отклонения свидетельствует о том, что цена актива может колебаться в широком диапазоне. Стандартное отклонение характеризует риск, связанный с данным активом. Чем больше величины отклонения, тем больше риск, и наоборот. Стандартное отклонение задается как процент отклоне- ния цены актива от ее средней величины в расчете на год. Напри- мер, если цена актива составляет 100 долл., а стандартное отклонение равно 10%, то это означает, что через год цена его может лежать в пределах от 90 долл. до 11О долл. (100±10%) в б8,3% случаев, от 80 долл. до 120 долл. (100±2х10%) в 95,4% случаях и от

70 долл. до 130 долл. (100±3х10%) в 99,7 случаях. Поскольку цена актива через год представляет собой результат действия рыночных сил, то она может и выйти за указанные пределы, однако в соот- ветствии с кривой нормального распределения 99,7% всех вероят- ных исходов лежат в пределах трех стандартных отклонений от среднего значения показателя, 95,4% — в пределах двух стандар- тных отклонений и 68,3% — одного стандартного отклонения (см. рис. 66).

Чтобы получить стандартное отклонение за период меньше года, необходимо стандартное отклонение в расчете на год разде- лить на квадратный корень из числа данных торговых периодов в году.

Пример. Стандартное отклонение бумаги равно 10% в год. Не-

обходимо определить стандартное отклонение в расчете на день.

В году насчитывается порядка 252 торговых дней. Поэтому стан-

дартное отклонение за один день равно:

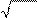10%:

252 = 0,63%

Если цена составляет 100 долл., то одно стандартное отклонение цены за день составит:

100´0,0063 = 0,63 долл.

На практике для расчета стандартного отклонения берут значе- ния котировочной цены. Западные аналитические компании, пре- доставляющие информацию о стандартном отклонении, рассчитывают его обычно на основе ежедневных значений коти- ровочной цены.

Формируя свои стратегии, инвестор пытается предугадать буду-

щее значение стандартного отклонения. В этом вопросе он ориен- тируется в первую очередь на фактические значения стандартного отклонения за истекший период времени, как минимум за послед- ний год. Помимо общего стандартного отклонения за год его интересует стандартное отклонение и за более короткие периоды.

Если он планирует заключить опционный контракт на небольшой

срок, то для него важна также информация о стандартном откло- нении за последний короткий период. Например, стандартное отклонение актива за год составило в среднем 20%, а за последний месяц 10%. Если инвестор планирует купить (продать) опцион на длительный период, то в расчетах ему следует учесть стандартное

отклонение, равное 20%, если же он заключает контракт на неда-

лекую перспективу, то значение отклонения в пределах от 20% до

10%, скажем, 15%, будет более верным, чем 20%.

Дата добавления: 2015-08-27