Дисперсия и ее свойства. Среднее квадратическое отклонение

Дисперсия (или варианса) - это средний квадрат отклонений вариант данной совокупности от их средней величины.

Дисперсия 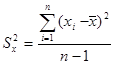или, если используется интервальный вариационный ряд

.

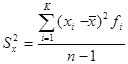Свойства дисперсии

Свойство 1. Если каждую варианту совокупности уменьшить или увеличить на одно и тоже постоянное число А, то дисперсия не изменится.

Упражнение 4. Доказать свойство 1.

Свойство 2. Если каждую варианту разделить (или умножить) на одно и тоже постоянное число А, то дисперсия уменьшится (или увеличится в А² раз.

Упражнение 2. Доказать свойство 2.

Среднее квадратическое отклонение определяется по следующей формуле:

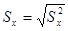. Чем сильнее варьирует признак, тем больше величина этого показателя и наоборот.

Дата добавления: 2015-08-27