Двойственная задача

В матричном виде задача, двойственная к задаче линейного программирования в общем виде, имеет вид: А^tY ³ C, Y ³ 0, V=(b,y) -> max.

Если взять двойственную задачу к двойственной, то получим исходную задачу. (Здесь А^t - транспонированная матрица).

ТЕОРЕМА. Задача линейного программирования корректна тогда и только тогда, когда исходная и двойственная задачи являются допустимыми. При этом минимум целевой функции в исходной задаче равен максимуму целевой функции в задаче двойственной.

Эта теорема позволяет вместо корректности задачи проверять два раза допустимость, что бывает заметно проще. Кроме того, важно, что ответы в двойственных задачах совпадают. Изредка, например когда имеем два неравенства со многими неизвестными, данная теорема позволяет перейти к случаю двух переменных и решать задачу графическим способом.

Напишем к задаче 2 двойственную:

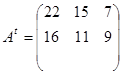, поэтому двойственная задача имеет вид: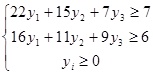

и в ней ищется максимум функции V = 200y₁ + 130y₂ + 75y₃

Упражнение: написать двойственную задачу к задаче 3.

Дата добавления: 2015-08-27