Симплекс - метод

Будем исследовать задачу линейного программирования в КАНОНИЧЕСКОЙ ФОРМЕ:

АХ = В, Х³ 0, f = (с, х) -> min.

При этом пусть A - матрица размером r*n, где r - число независимых уравнений, n-число переменных, r<n, rang(А)=r.

Заданная система имеет бесконечно много решений, при этом множество решений системы образует пространство размерности n-r. Чтобы его описать, надо выбрать n-r свободных переменных, тогда оставшиеся r переменных будут называться базисными и выражаться через свободные переменные.

Договоримся, что свободные переменные имеют номера с r+1 до n-ого, т.е. базисными переменными являются x₁,...,x_r.

Выразив базисные переменные через свободные, линейную систему сведем к виду:

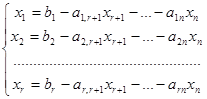Если свободным переменным придать значение, равное 0, то получим решение: (b₁,b₂,...,b_r,0,0,...,0).

В каком случае этот набор будет допустимым решением задачи? Так как х_i должны быть неотрицательными, то и все b_i должны быть неотрицательными. Такое решение задачи называется базисным решением. Базисных решений много. Геометрический смысл базисного решения состоит в том, что это координаты одной из вершин многогранника допустимых значений в n-мерном пространстве. Если задача корректна, то одно из базисных решений задачи будет оптимальным. Следовательно, перебирая все вершины и вычисляя значение целевой функции в каждой из них, мы можем найти решение задачи. Однако, данный процесс очень трудоемок: для нахождения одного базисного решения придется решать систему уравнений r*n (а количество базисных решений равно числу сочетаний из n по r, т.е. весьма велико).

Симплекс-метод служит для облегчения процесса перебора: он заключается в последовательном переборе части базисных решений. Перебираются не все решения подряд, а только такие, что на каждом последующем шаге значение целевой функции становится лучше.

Дата добавления: 2015-08-27